Most people who play Roulette make contact with betting strategies at some point, e.g., the famous Martingale system. But what about the Reverse Martingale Strategy? Does this work at all for Roulette?
The Reverse Martingale strategy for Roulette has a probability structure less favorable than the Martingale system. The main advantages of the Reverse Martingale system over not using a betting strategy is the low amount of cash required at the start and a higher average amount of cash at the end – if the player keeps winning.
While the basic idea of the strategy is simple and seems doomed somehow on first glance, the details are quite intricate. And I myself would have never thought that I had that much to share in this article, but I stand corrected. So bear with me and get ready to be surprised! All details follow below.
At this point, I strongly urge you to take a look at my simulation disclaimer. After you have read the simulation disclaimer, you’ll know better (I hope) what to make of the information contained in this article and what not to conclude from it.
Betting Strategies in Roulette
Roulette is a game of chance played in casinos. Since people go there to play with money, and in order to ideally win some, it is tempting to assume that there are strategies for playing Roulette, for example, in such a way, that a win would be guaranteed.
However, there is no strategy to win for sure in a game of chance. Most people know this, but still want something useful to follow. And thus, there are strategies or systems that people follow when they play in a casino.
For Roulette, there are several betting strategies. Since the goal of a betting strategy apparently can not be to win for sure, the next best thing is to have a strategy that promises a high probability for winning. If we approach the topic of betting strategies this way and keep up a scientific point of view, we can actually make a number of interesting and even helpful statements about a particular game or system.
In this article we look at the so-called Reverse Martingale Strategy. What is meant by Reverse, and how does that differ from the Martingale Strategy?
The Steps in the Reverse Martingale Strategy
The steps in the Reverse Martingale betting strategy are as follows:
- Set a base amount, i.e., a starting bet that you are going to use. Example: 10 $.
- You are betting on something where you win or lose the amount you bet in every round. Example: You bet 10 $. If you win, you get your bet back plus the amount that you bet, so another 10 $. If you lose, you lose your bet entirely, so, in our example, your 10 $.
- The system uses a betting progression. In particular, the basic rule is:
- if you win, you double your bet in the next round
- if you lose, you go back to the base amount, no matter how many times you won in a row before that.
- Before you start playing, you decide on a particular number of subsequent wins or a desired amount won in one progression, after which you’ll reset the progression back to the starting amount, in addition to the previous rule.
This target number of steps in the progression essentially represents the level of risk that you are taking. The act of resetting the progression corresponds to “walking away” with your win, even if you keep playing by starting over at the base amount.
Sounds complicated? Actually, it isn’t that complicated. Here is an example of what can happen to your amount of cash in hand, when you do this. I’ll explain more about the simulation below, but for now, I show you a single possible outcome of his strategy in action (in this case, a really lucky one):
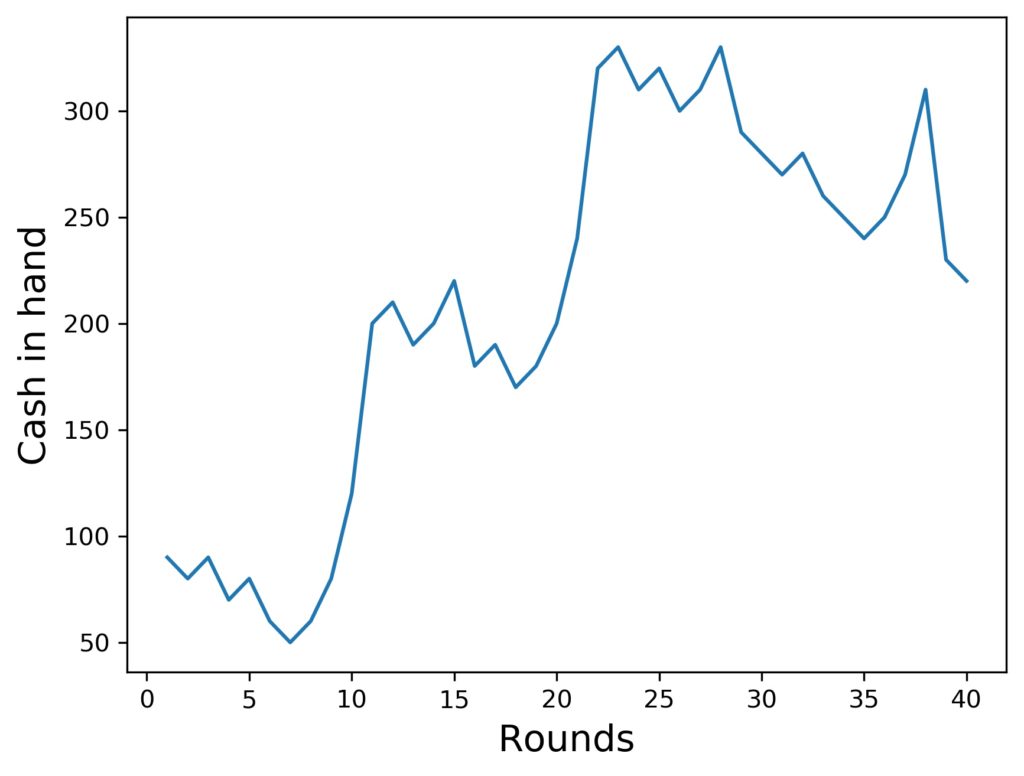
A little explanation is in order, though: This simulated player started with 100 $, simply because it is easier to generate a useful picture this way. As you can see, the player lost a couple of times before the first big win, and then, shortly thereafter, even a second big win occurred.
This player is using 4 steps as the target. If she or he wins 4 times in a row, they stop the progression and bet the base amount again. This can be nicely seen in the graph above, where after the large wins, in both cases the player won one more time, but got only the base amount back.
Wow, that looks nice, doesn’t it? However, as I already mentioned, this was a very lucky simulated player. Here is another example, who was less fortunate:
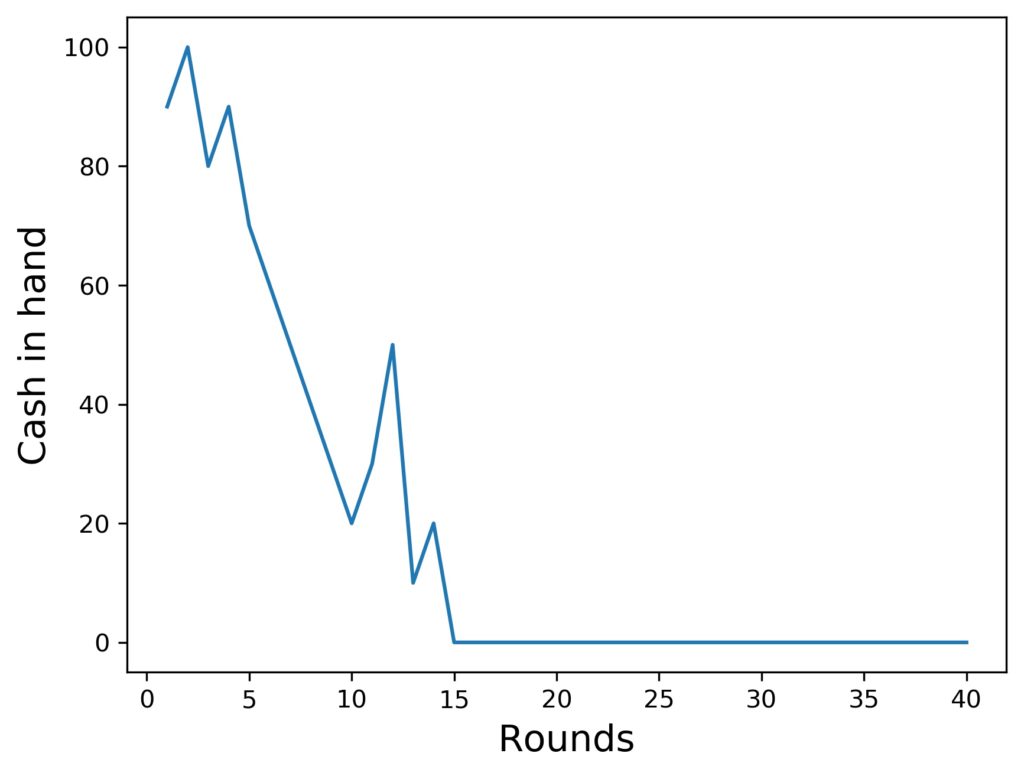
This simulated player started at the same amount and played with the same tactics, but lost all their money after 15 rounds. You’ll see whole collections of these curves further down, but before that, I’d like to make clear really quickly, what the differences between the Martingale system and its Reversed version are.
What is the Difference between the Martingale and the Reverse Martingale Strategy in Roulette?
There are two important differences between the Martingale and Reverse Martingale strategies in Roulette: First, for Reverse Martingale the player doesn’t need a lot of cash to start playing with the system, while in Martingale one does. Second, the doubling/returning-to-start-bet behavior after a win or a loss are reversed between the two strategies.
In more detail, in the Reverse Martingale system you
- can start playing with any amount of cash (as long as it is more than the table minimum, of course)
- bet the base amount after a loss
- double your bet after a win
- stop the progression after a number of steps, which has been fixed before you start playing
In the Martingale system, on the other hand, you
- can only start playing with enough cash in hand to support the number of steps in the progression that you have planned
- bet the base amount after a win
- double your bet after a loss
- never stop the progression, but keep doubling until you lose everything
In effect, in the Martingale strategy you try to recover subsequent losses by the doubling-up progression, while in the Reverse Martingale you try to win some credit by being aggressive, and lose it back to the bank afterwards.
The Progression steps in the Reverse Martingale System
The reverse Martingale strategy has a simple progression. Every time you win, you double your bet. Starting with 10 $, the steps are the following:
| Step | Bet = Possible Win = Loss if loss occurs at this round | Probability for winning n subsequent steps for 50/50 chance at each step, in percent, rounded |
|---|---|---|
| 1 | 10 | 50 |
| 2 | 20 | 25 |
| 3 | 40 | 12.5 |
| 4 | 80 | 6.25 |
| 5 | 160 | 3.13 |
| 6 | 320 | 1.56 |
| 7 | 640 | 0.78 |
| 8 | 1280 | 0.39 |
| 9 | 2560 | 0.20 |
| 10 | 5120 | 0.10 |
| 11 | 10240 | 0.05 |
| 12 | 20480 | 0.024 |
So there is not much to think about or keep track of, except for how high the bet currently is and whether or not you should reset the progression.
Playing the Reverse Martingale System in Roulette
So, now that we know what the Reverse Martingale system is and how it is supposed to work, let’s look at how it does at the Roulette table.

As mentioned above, you are looking for a kind of bet, where you win back the amount of money that you bet, or you lose your bet completely. This is the case for the black versus red or odd versus even bets in Roulette, for example. Fine, so the system can be applied to any of those.
One thing to always keep in mind in a casino is the house edge. This means that while win and loss are equal for such a bet, the winning and losing odds actually aren’t. In Roulette, there are 36 numbers to bet on that are also red or black, and odd or even, respectively.
However, there is an additional number 0 in the European variant, and there are two additional numbers 0 and 00 in the American variant of Roulette, that are separate and don’t belong in either of those categories. As a result, the odds for winning a bet on, e.g., red are 18/37 in European and 18/38 in American Roulette.
Still, the house edge is more like a general but small disadvantage that players face in casinos. It doesn’t play a huge role for the analysis of betting strategies like the Reverse Martingale system, however. I’ll show you a comparison of probabilities with and without a house edge further below, but for now, we’ll concentrate on the major points of the Reverse Martingale system.
So, essentially, what you do is to just leave the chips there after a win to bet the previous bet plus the win again, until you reach the number-of-steps limit in the progression. Then you take your win and bet the base amount again. If you won, that is. If you lose at any step, bet the base amount.
The Role of Streaks in the Reverse Martingale Strategy for Roulette
What people often write about the Reverse Martingale strategy in Roulette are things like that the player “tries to make use of a streak” or “needs to know when to stop” or “walk away at the right moment”. Unfortunately, these statements are dangerously misleading.
There are no actual streaks in Roulette (or any other game of chance by the way). Which doesn’t mean that you cannot call a sequence of 8 times red a streak. However, it means that all spins of the Roulette wheel are completely independent of each other, and random. We cannot predict the next number on the basis of the known past number sequence.
Interestingly, all betting strategies respect that in the sense that the player does not need to rely on instinct or experience or whatever to guess the next number or know when to stop. A betting strategy is just a set of rules that has statistical consequences (and we’ll investigate those statistical consequences below). Any statement to the contrary should be taken with a barrel of salt.

To make my point even stronger and show you how not-streaky these strategies actually work, here is an interesting fact about playing the Reverse Martingale:
Usually, for a system like this you are told to pick a color like red and stick to it. Only bet on red, all the time. You can do that, it is fine, but not necessary. The actual criterion for using the system is this: Always bet on any outcome of an event where you win your bet back and have an almost even chance of winning. That’s it.
So, in Roulette, you can bet red red black odd black even even odd red red odd or anything like this, and still correctly use the Reverse Martingale system. If that surprises you, you see and feel, how deeply rooted our beliefs in streaks and dependences of actually independent events are in our minds.
But enough talk, let’s get back to the pictures. Before I can do that, I need to shortly explain to you where they come from.
Using Monte Carlo Simulation in Order to Study Roulette
Monte Carlo simulation is a numerical technique to study the behavior in complex systems. The practical part about it is that not much about the system needs to be known. In the case of Roulette, we need to know the possibilities of what can happen at every spin, e.g., which numbers or colors occur with what probabilities.
If this is known, we have the computer run and play through a large number of simulated games. The numbers are drawn by a random number generator, and the results for each run are recorded and evaluated statistically. Of course, we can also make figures from such runs, as you have already seen above.
The powerful thing about Monte Carlo simulations is that they produce controlled estimates of probabilities of certain outcomes, like “lose everything”, including an estimate of the numerical error. In the end, all we do is make sure that the numbers are reliable and be careful when we interpret them.
Typical Outcomes of the Reverse Martingale Strategy When Playing Roulette
We have seen two typical outcomes of the Reverse Martingale strategy in Roulette above. As you can imagine, studying thousands of outcomes like that (one by one) would take a very long time and be rather confusing. So here is a better way. The following figures show you several runs at once, for the same base bet.
There are several interesting parameters to study:
- the amount of cash the player has in the beginning
- the number of steps in the progression, which they have restricted themselves to
- which variant of Roulette is played (European or American), or whether or not we ignore the house edge completely
- what the table maximum is, if there is one (which there always is in a real casino).
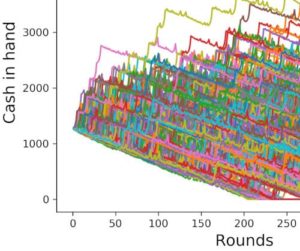
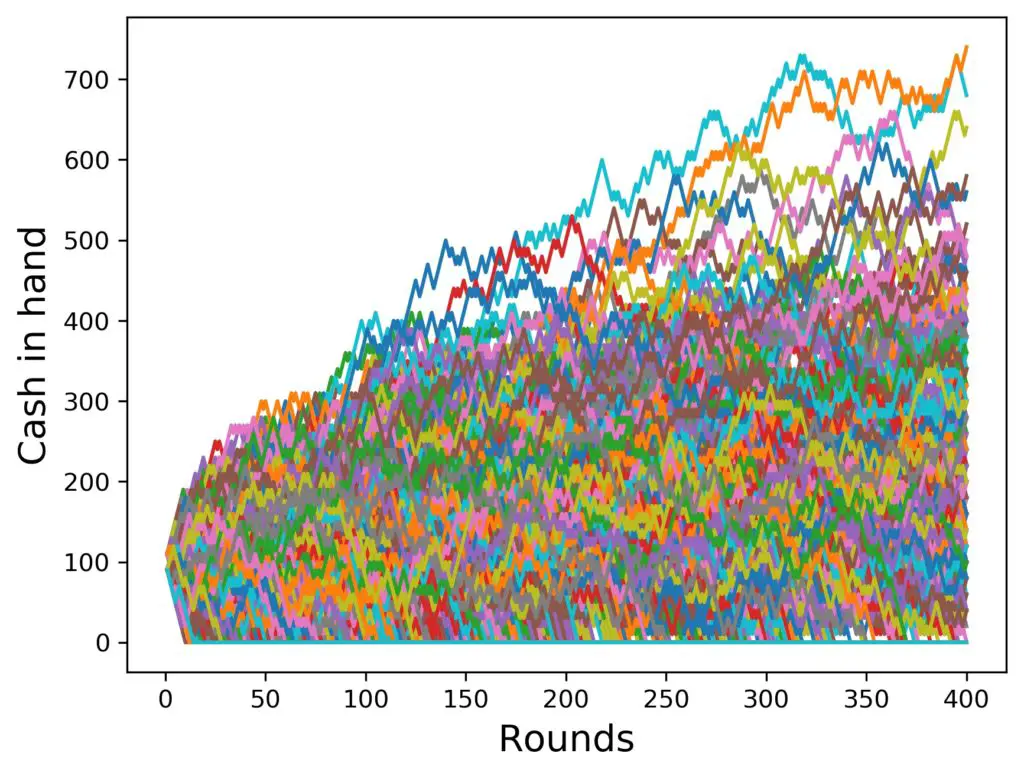
Let’s start off with a starting amount of 100 $, the base bet is 10 $, and we go up to 4 steps in the progression before resetting. For European Roulette without a table limit, we get the following for 100 simulated players playing up to 40 rounds of Roulette (which is roughly an hour):
This is perfect to see what happens on average in a group of players of this size:
- a large number of players gt a small win occasionally or even a couple of times, but lose all their money rather quickly
- some players get one big win (which means that they get to their target step count once), but then they keep losing and their cash goes down gradually.
- some fewer players get two big wins and go back down after that
- some even fewer players get three big wins, go down after that, and so on.
- the big wins can also occur at various times which produces the little transgressions from one “main downward band” to the next.
- In this particular sample, one lucky player went up four times during 40 runs and got to like 600 $.
Open questions (at least for me):
- How important is the starting amount?
- How important is the number of steps to the target win?
- When has everyone lost everything?
- What happens if we plot more runs?
- What happens over longer periods of time?
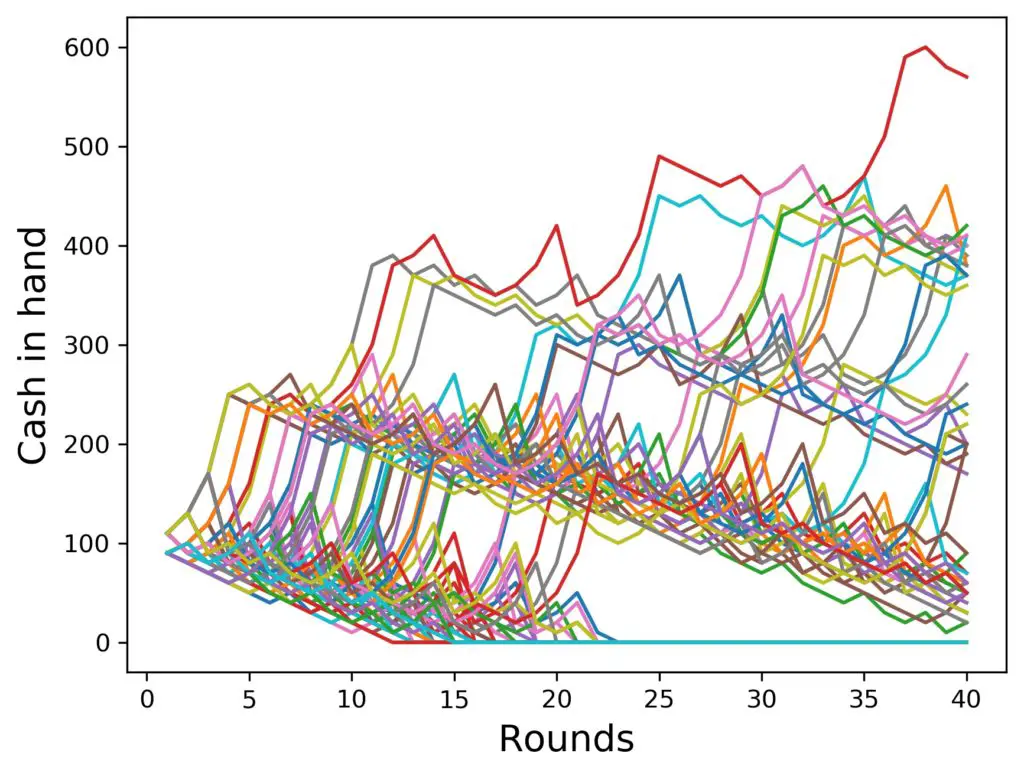
Let’s now try to answer these questions, shall we? Game duration first. Let’s increase the run time to 400 rounds (that amounts to roughly 10 hours of playing non stop in a casino):
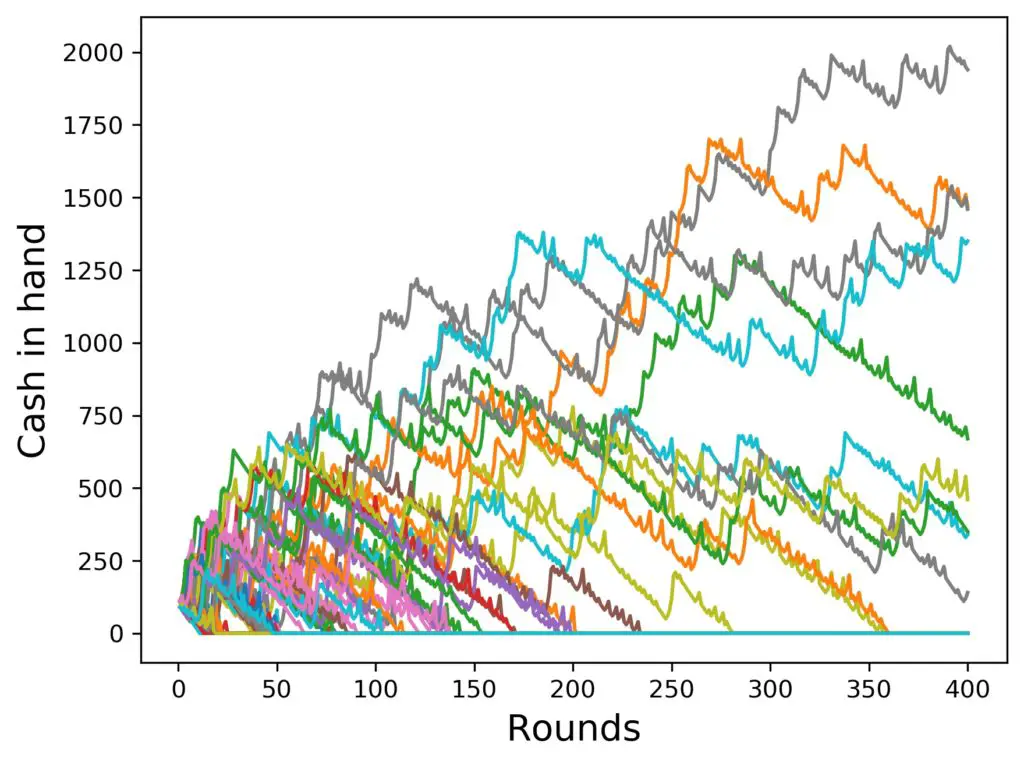
Well, there are a couple of observations to be made:
- only a handful (in this case 9) of the 100 players survive 400 rounds.
- the wins for the luckiest ones can get quite substantial, like 2000 $ compared to 100 $ in the beginning
- most people lose 100 $ easily at Roulette in a day
Dependence of Outcomes on the Number of Steps in the Reverse Martingale Progression
Now, what happens, if we allow two more steps in the progression? Here we go:

Whoa. If it weren’t for the blue curve on top, the situation would look really dire with 6 steps in the progression as compared to 4 steps. Since things are difficult to average over, when there are only a few of them, let’s create the last two charts again, but with more players each, like 1000, i.e., 10 times as many. Here is the situation:
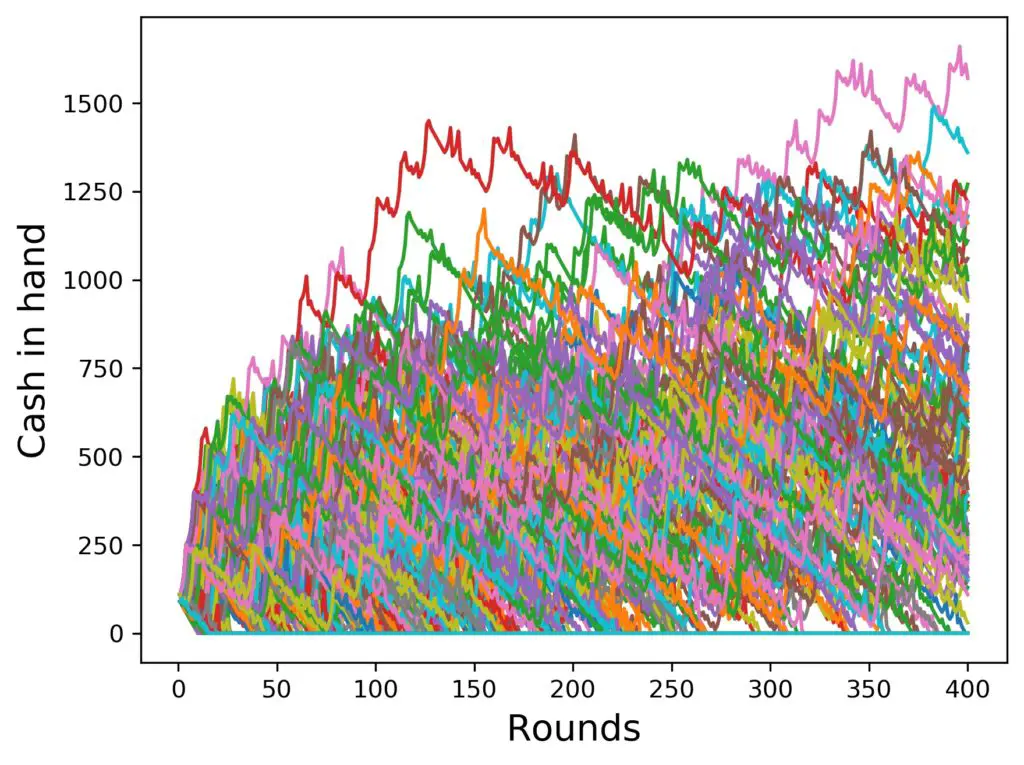
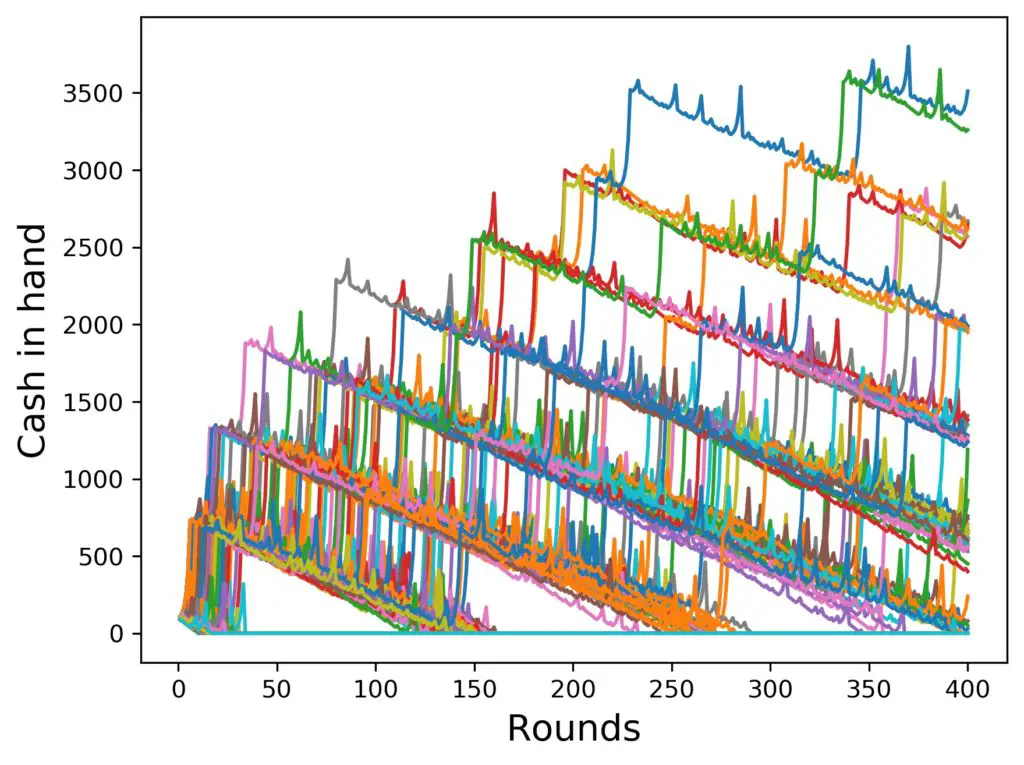
What we observe here is that
- the curves can go higher up, if more steps are taken
- much fewer simulated players get “lucky”
- the “band” structure in the runs is much more prominent for 6 steps, which emphasises that a simulated player rarely wins big and just goes down losing most of the time in between the big wins
And what happens, if we use fewer steps in the progression, like 3 or even only 2? Here are the results, for 1000 simulated players each, starting from 100 $:
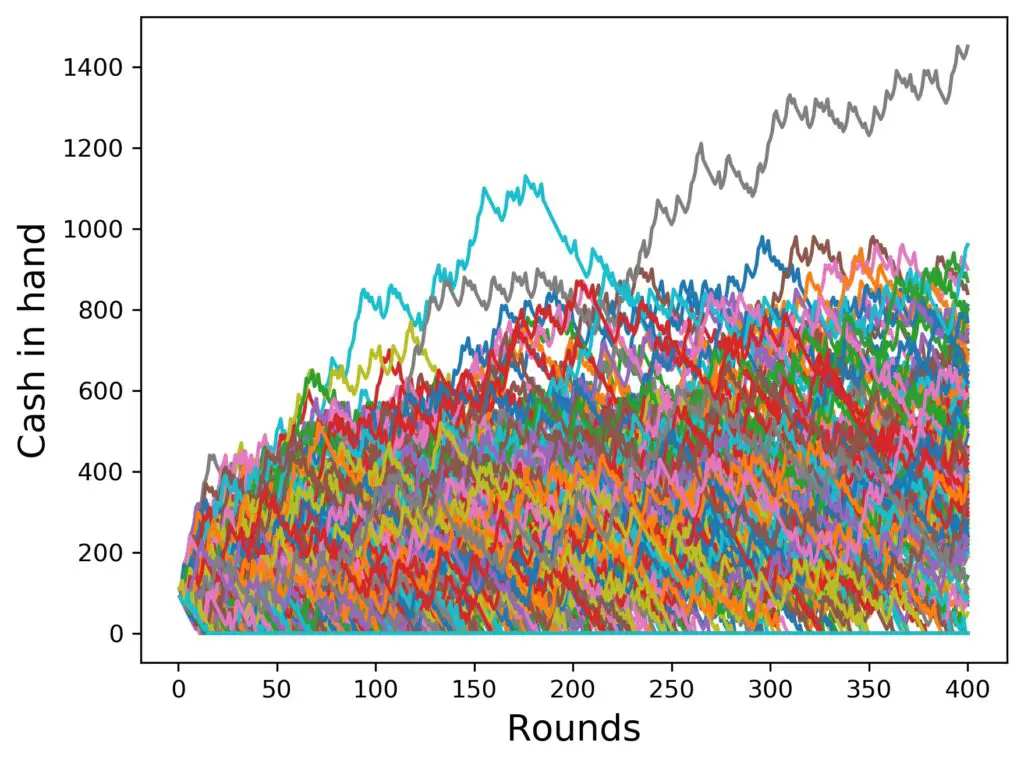

The pattern continues: the top amounts in hand get smaller with the number of steps in the progression, but the whole figure is densely populated. By the way: also the line at zero is densely populated, but only shows one line. The average amount of cash is going down steadily with every round, although the figure seemingly has a large bump above the starting amount of 100 $.
And what about a single step in the progression? That corresponds to just betting the same amount on red, black or the like all the time. No progression, no system. That is what it looks like:
Dependence of Outcomes on the Starting Amount in the Reverse Martingale Progression
The starting amount of cash is another interesting parameter in this simulation. In the pictures you have seen so far in this article, I have started the simulations with 100 $ cash in hand, which is 10 times the base amount in the progression. I did this in order to be able to show you something without having to try too often to produce a reasonable figure. In this section, you’ll see why, but not just that.
100 $ starting cash is a reasonable amount to start playing with, but what if we don’t have 100 $, but only 50 $? Or even less? One of the strengths of the Reverse Martingale system is, in fact, that you can start playing with only 10 $, i.e. one time the base amount in our hands at the beginning. But how successful is that going to be? Let us find out.
In the next couple of figures, I’ll show you the same setup, Reverse Martingale, 1000 simulated players, 4 steps in the progression, up to 400 rounds, but I’ll gradually lower the amount of cash at the start. To have a reference, we start at 100 $, then go down in steps of 20 $, and finally also add the one for 10 $ only. I am curious. Here we go:

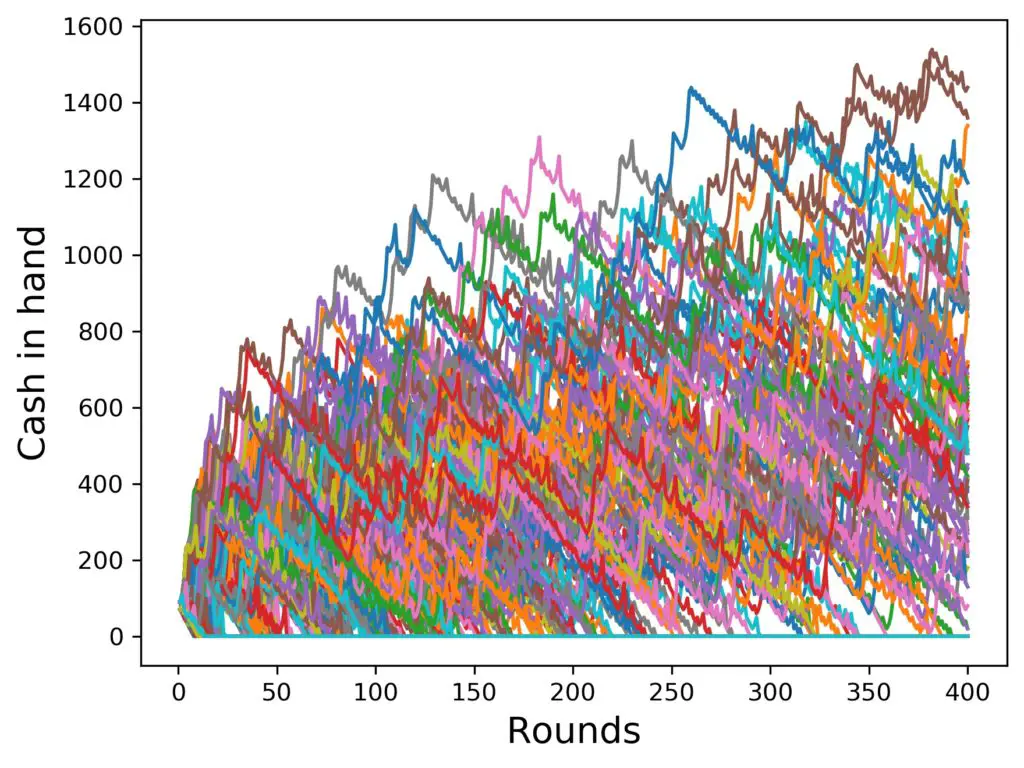
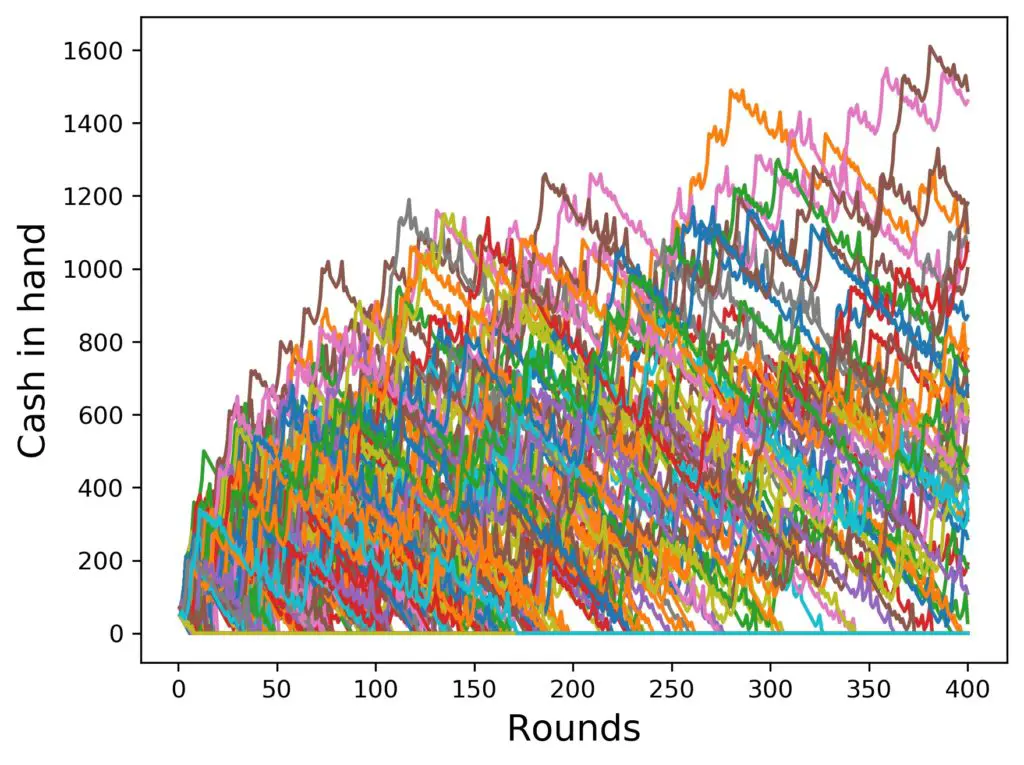
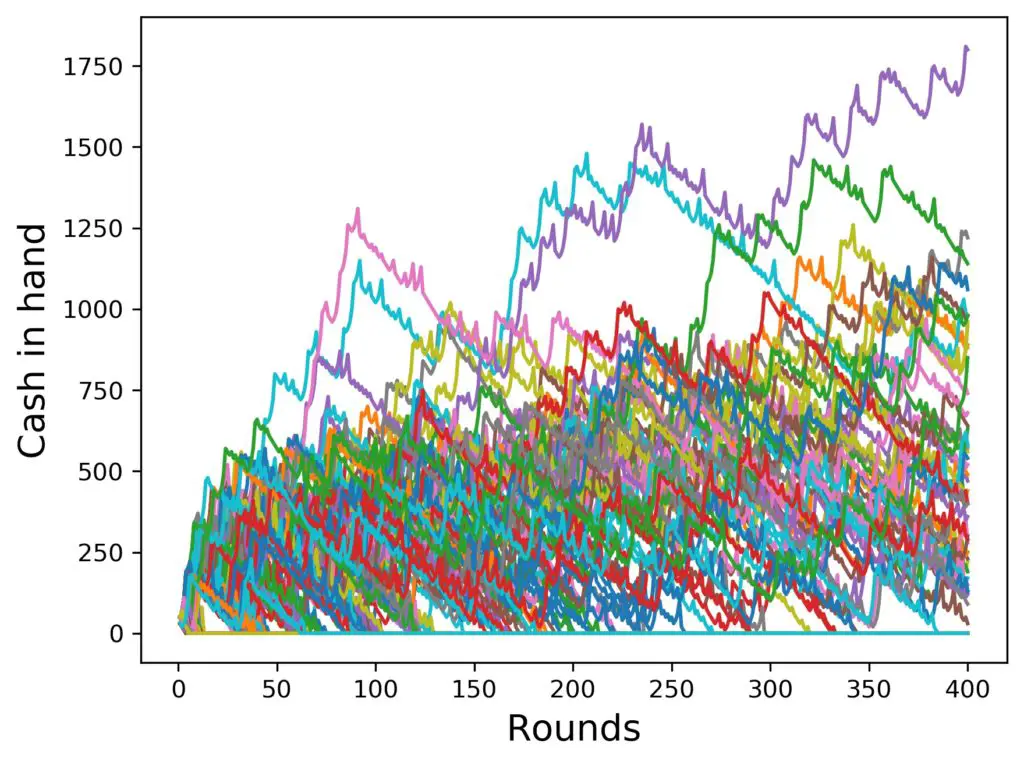
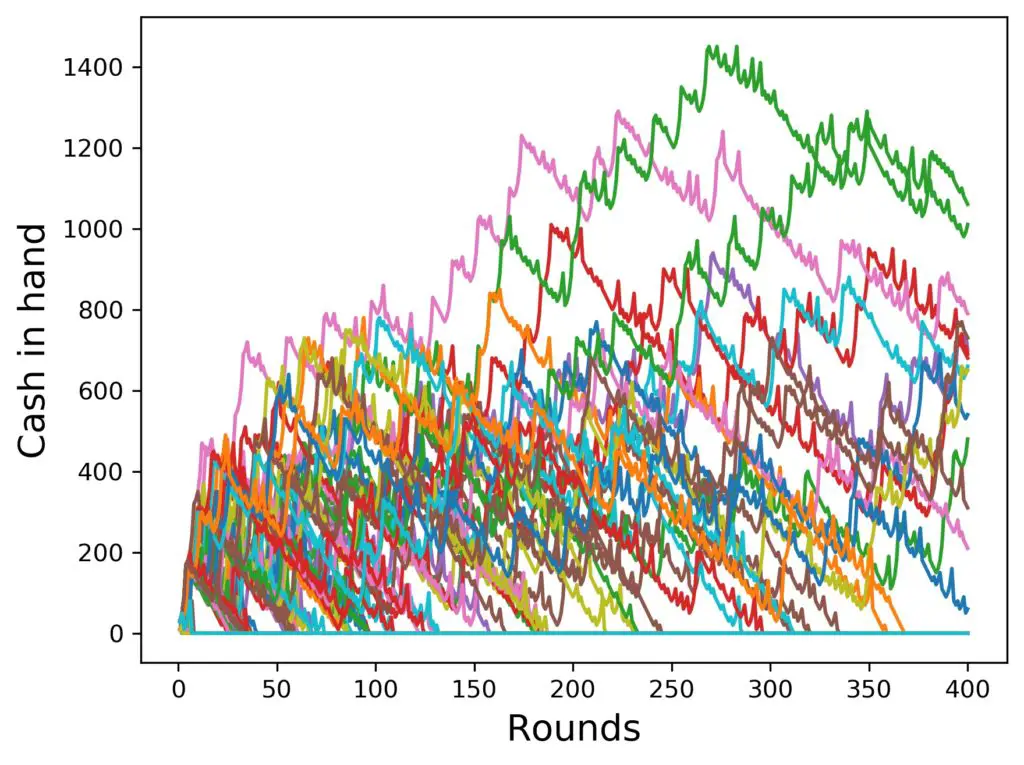
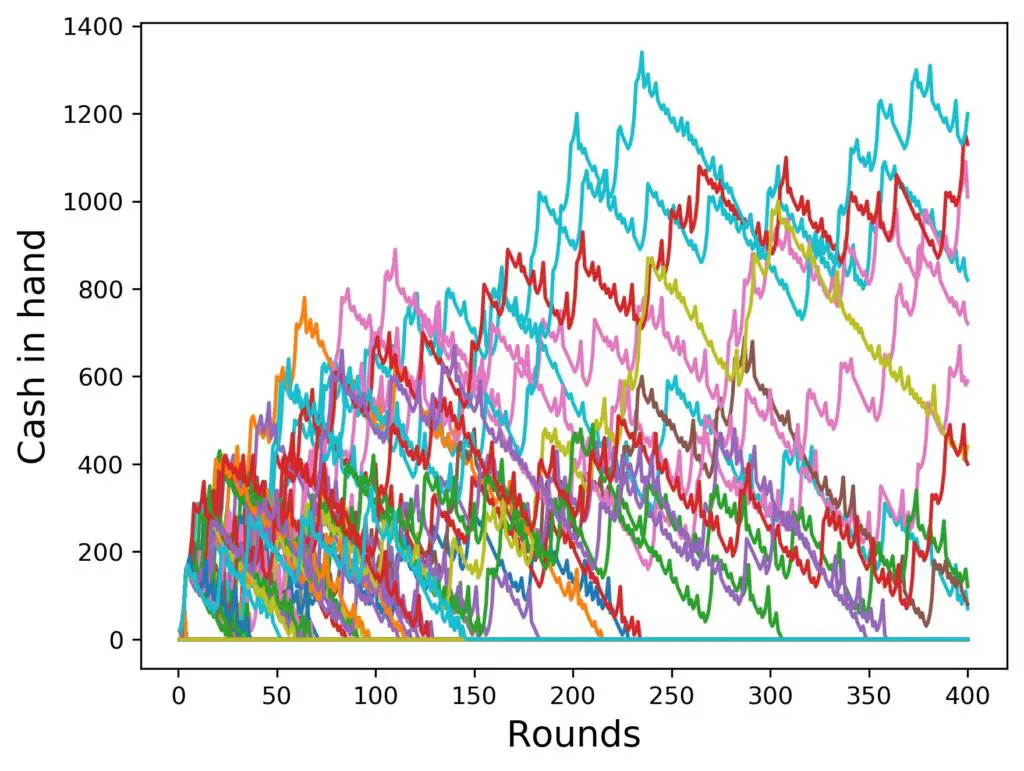
Well, that could have been worse, but also better. But does the strategy actually help as compared to just betting the same amount all the time, if you have only 10 $ to begin with? Let’s have a look. Here is the last figure again on the left, and on the right a simulation with only one step in the progression (i.e. no progession at all):

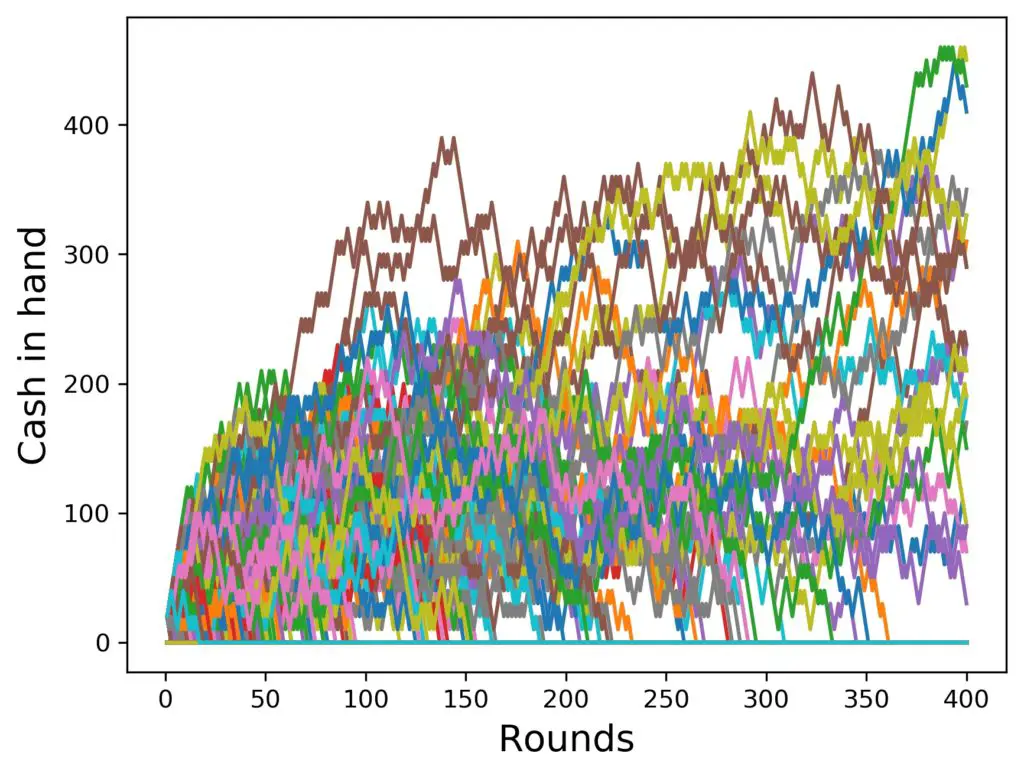
Looks like for more progression steps, the winnings are higher (if you win at all, that is), but a lot more people survive 400 rounds without progressing.
Actually, it helps to look at the average cash that all simulated players have left after 400 rounds as well as the averaged probability for losing. Would you believe that these two plots are almost the same in both regards?
Within reasonable errors, the average cash after 400 rounds with 4 steps is roughly 5 $, with 1 step it is roughly 4 $. The probability for having a net win after 400 rounds with 4 steps is 0.8 percent, and with 1 step is 1.9 percent.
And before you say wait, that’s more than twice as high a probability: the other side of the coin is that the probabilities for losing everything are 99 and 98 percent, respectively. That doesn’t look like a big difference, at least to me. We’ll get into the details of the various probabilities soon.
The Effect of a Table Maximum on the Reverse Martingale Strategy in Roulette
Before I go into the discussion of probabilities, I would like to quickly mention the effect of a table maximum on the use of the Reverse Martingale strategy in Roulette.
I say quickly mention, because the situation is much simpler than, e.g., in the related case of the Martingale strategy, where a table limit effectively stops the progression at some point, in particular during longer games. For the Reverse Martingale system, however, the progression is restricted a priori by the number of steps that the player chooses to follow.
Conveniently, one can choose the number of steps such that the bet will never reach the table maximum. If the maximum is 150 dollars, that’s exactly 10 $ lower than the bet at step 5 of the Reverse Martingale progression with a base amount of 10 $, so you can use 4 steps. If the maximum is 1000 $ you could in principle go up to 7 steps, which means a bet of 640 $ but rather low odds already (see the table above).
However, the question is whether you should do that in the first place. The restriction on the number of steps is a more important one than the table limit for the Reverse Martingale strategy in Roulette.
The Effect of the House Edge on the Reverse Martingale Strategy in Roulette
Whenever we play in a casino, we have to live with the house edge. But how important is that edge for betting strategies like the one discussed here? The short answer is: not too much.
The reason is somewhat buried in the probabilities for winning or losing at the Roulette table, which is why we are going to look at them now in detail.
As our first example, let’s use 4 steps in the progression and a starting amount of 100 $. The base bet always remains at 10 $. For these kinds of figures, I simulated 20 samples of 10 000 players each, in total 200 000 simulated players. This makes the probabilities reliable enough for our discussion.
With the European house edge, this looks like the following chart. The blue curve is the average probability for losing everything after the corresponding number of rounds. In orange, you see the probability for a net loss (compared to the starting amount), and in green you see the probability for a net win (compared to the starting amount). The green curve, by the way, also includes the rare cases where a player arrives at exactly the starting amount again after so and so many rounds.
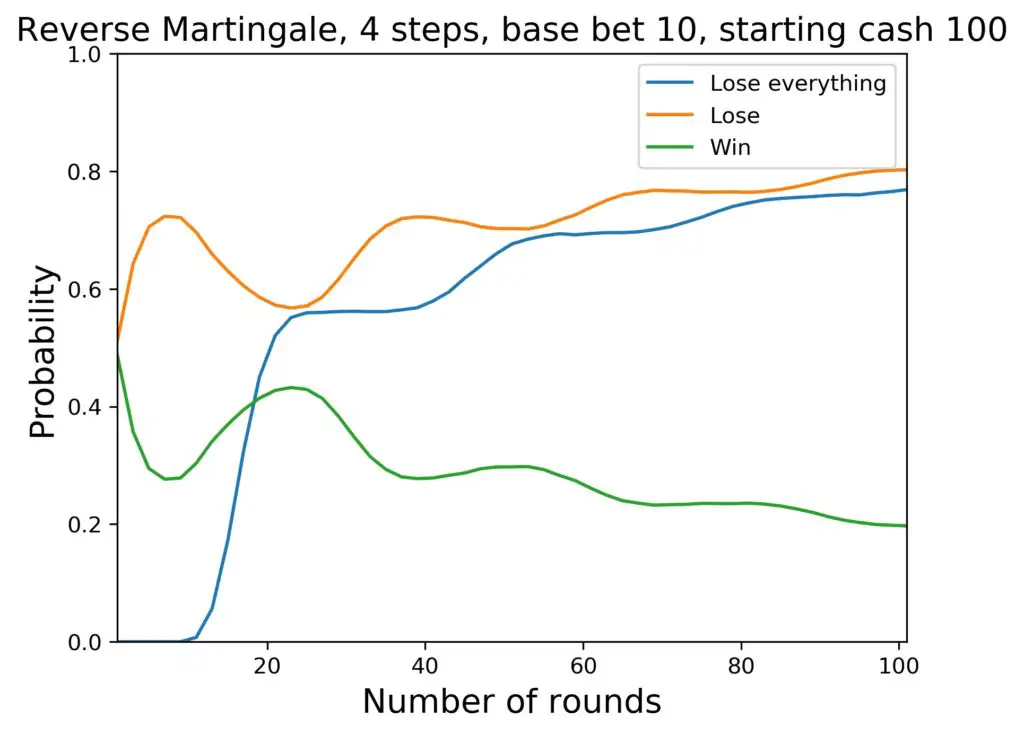
So far, so good. What happens, if we remove the house edge? Here we go:
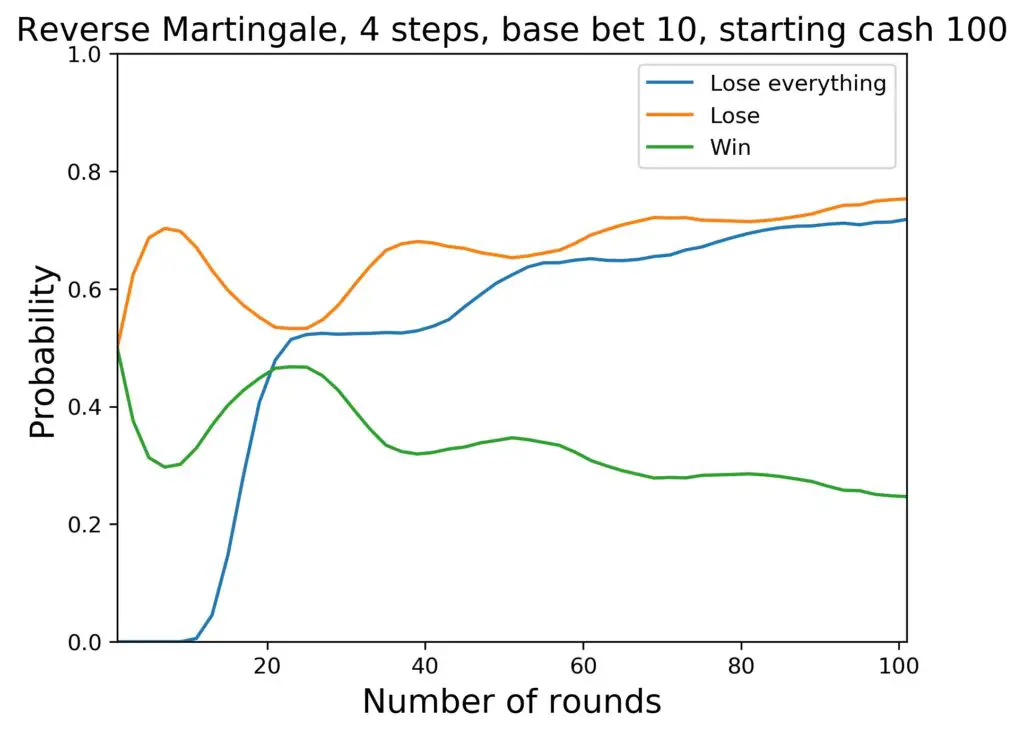
What’s the difference? Nothing monumental, as already mentioned, but we can see the probabilities for a net win and a net loss come closer together without the house edge. More precisely, the winning probability goes up and the losing probability goes down.
In numbers for the average cash after 100 rounds, this means 100 $ without the house edge, and 75 $ with the European one. And, since we can easily switch to the American Roulette system as well, the average cash after 100 rounds with this system there is 56 $. Here is the corresponding figure:
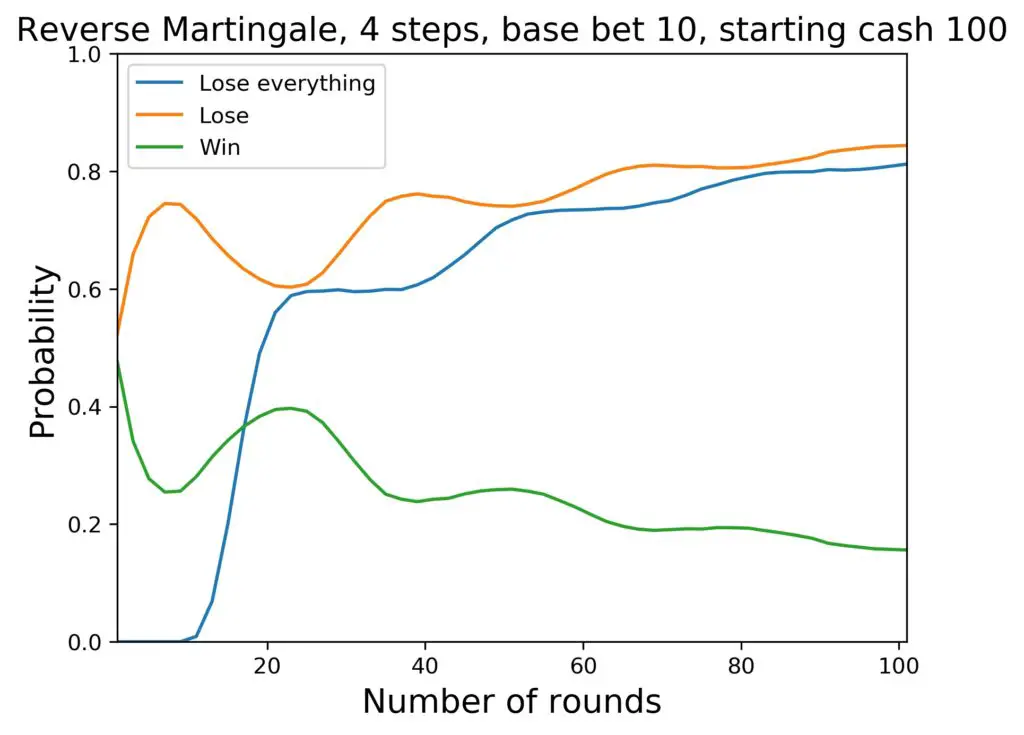
With shrinking winning probability for every single round, the probability for a net win goes down, and the probability for a net loss goes up.
Probabilities for the Reverse Martingale Strategy in Roulette
An interesting question to ask for any particular betting system is the following: after how many rounds do I have the highest probability of winning, and how high is it? Or: how probable is a total loss after a given number of rounds at the table?
In order to investigate questions like these, the kind of plots we just saw are ideal. Let’s stretch the range a bit, and go up to 400 rounds of playing. Then we’ll look at the effect of the various other variables in the system, but always with a house edge, and not considering table maxima separately, because they have been sufficiently covered.
We’ll also stick to the American version of Roulette, because it is the most disadvantageous for the player. Things can only go up from there. So here is the first plot. 4 steps in the progression, 100 $ to start with, and 400 rounds, which corresponds to roughly 10 straight hours of playing.
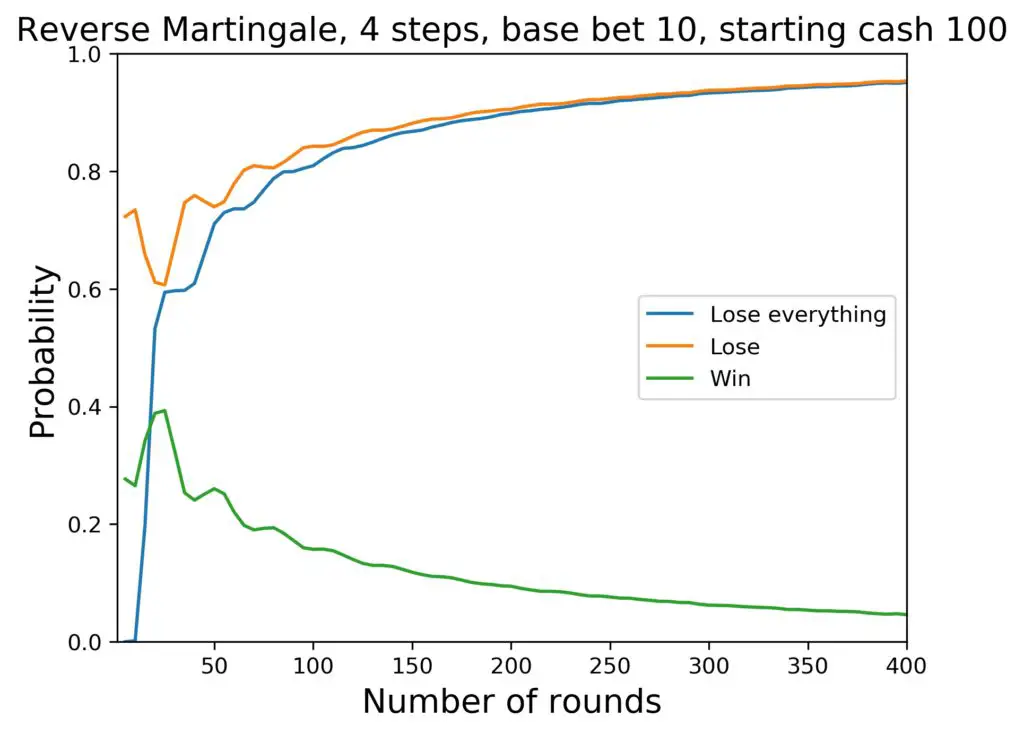
The following data are of interest (amount and percentages are rounded):
- the average cash at hand after 400 rounds is 26 $.
- the probability for a total loss is 95 percent
- the probability for a loss is 95 percent
- the probability for a win is 5 percent
So what do we observe here? The following things appear to me:
- At no point in time, the probability for a net win goes above 50 percent. If you want more details on the first few rounds, look at the previous figure.
- There are some oscillations in the probability curves that go back to the number of steps in the progression. Only after a full progression can actually have been completed, the system can also feel the effect.
- The curve for a total loss rises rather quickly at the beginning and approaches the curve for any net loss fast and closely.
- After a short amount of time, almost any loss is total.
Dependence of Probabilities for the Reverse Martingale Strategy in Roulette on the Number of Progression Steps
Now what could we change? The number of steps in the progression, for example. For 6 steps in the progression, the situation looks like this:
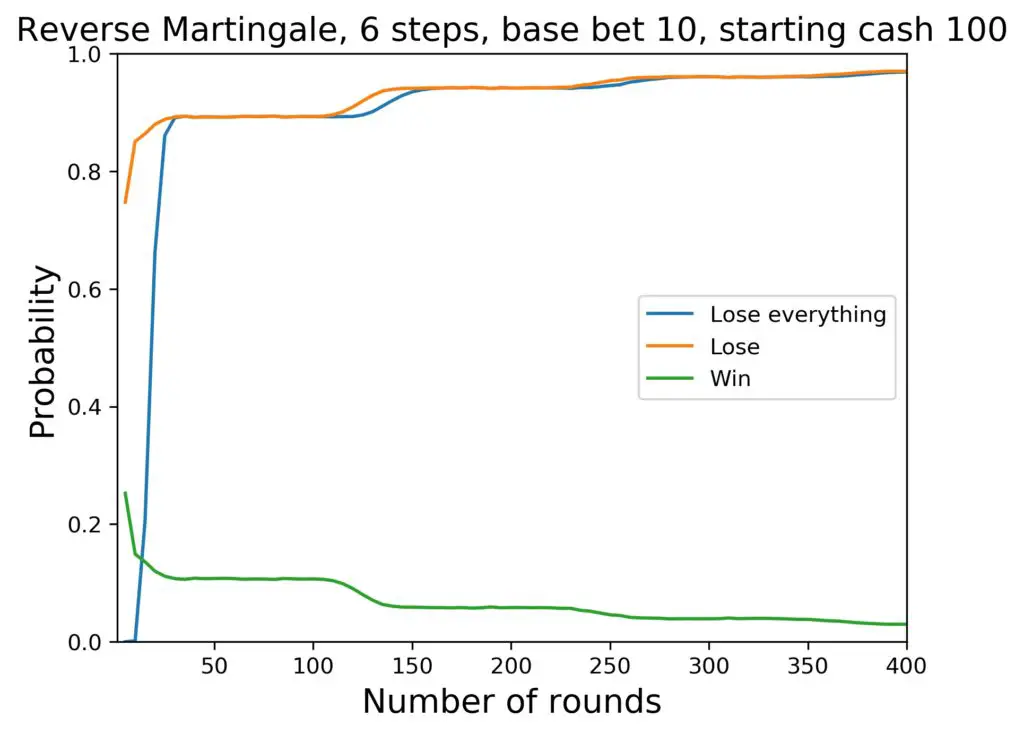
The following data are of interest for this run (amount and percentages are rounded again):
- the average cash at hand after 400 rounds is 36 $.
- the probability for a total loss is 97 percent
- the probability for a loss is 97 percent
- the probability for a win is 3 percent
So what do we observe here?
- The winning-losing margin has become more pronounced.
- The losing probability seems to rise with the number of steps in the progression.
- The average cash in hand after 400 rounds has gone up, however.
What if we lower the number of steps in the progression from 4 to 2? Here ist what happens up to 400 rounds:
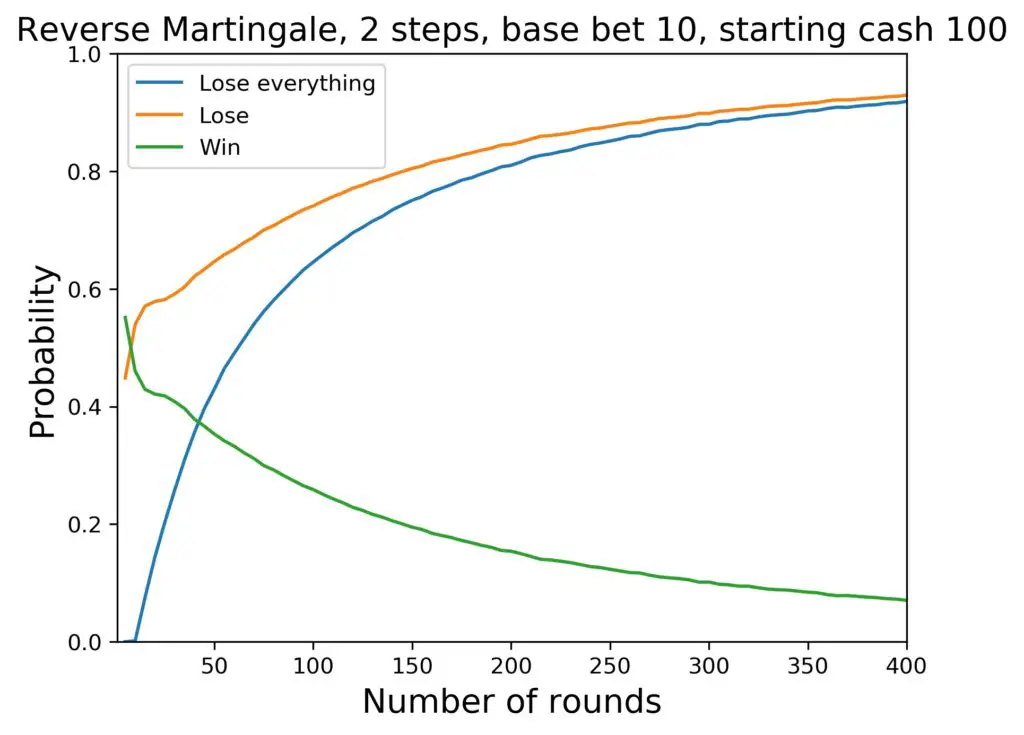
Here are the key data of interest again for this run (amount and percentages are rounded):
- the average cash at hand after 400 rounds is 21 $.
- the probability for a total loss is 92 percent
- the probability for a loss is 93 percent
- the probability for a win is 7 percent
Observations from this additional case are:
- The oscillations are much less pronounced.
- The winning probability has gotten better.
- We can tell apart the probabilities for a total loss and any net loss.
- There seems to be a region in the beginning, where a net win is more probable than a net loss! We need to look at this more closely!
Here is the same setup again, but with better resolution for the first 40 rounds:
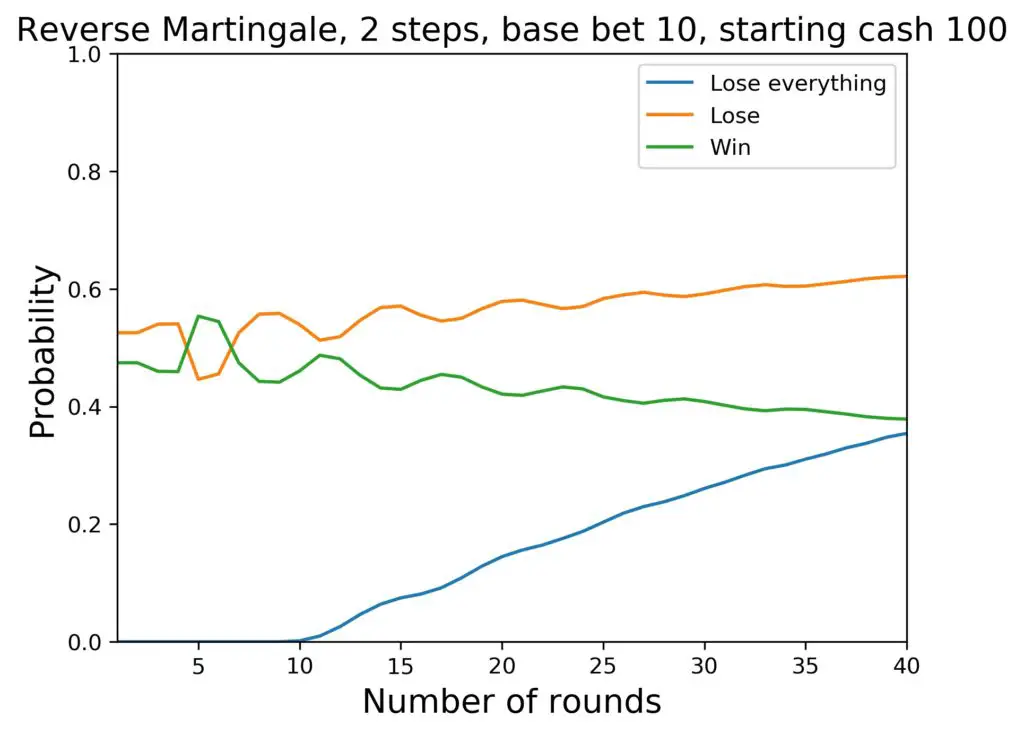
Aha! So that means that with this setup (100 $ to start with, 2 steps in the progression), we get a small net-win probability after 5 and 6 rounds. And that is all.
Finally, let us set a baseline with the 1-step setup, i.e., we ignore the progression completely and bet just the base amount every single time. What happens then, is the following:
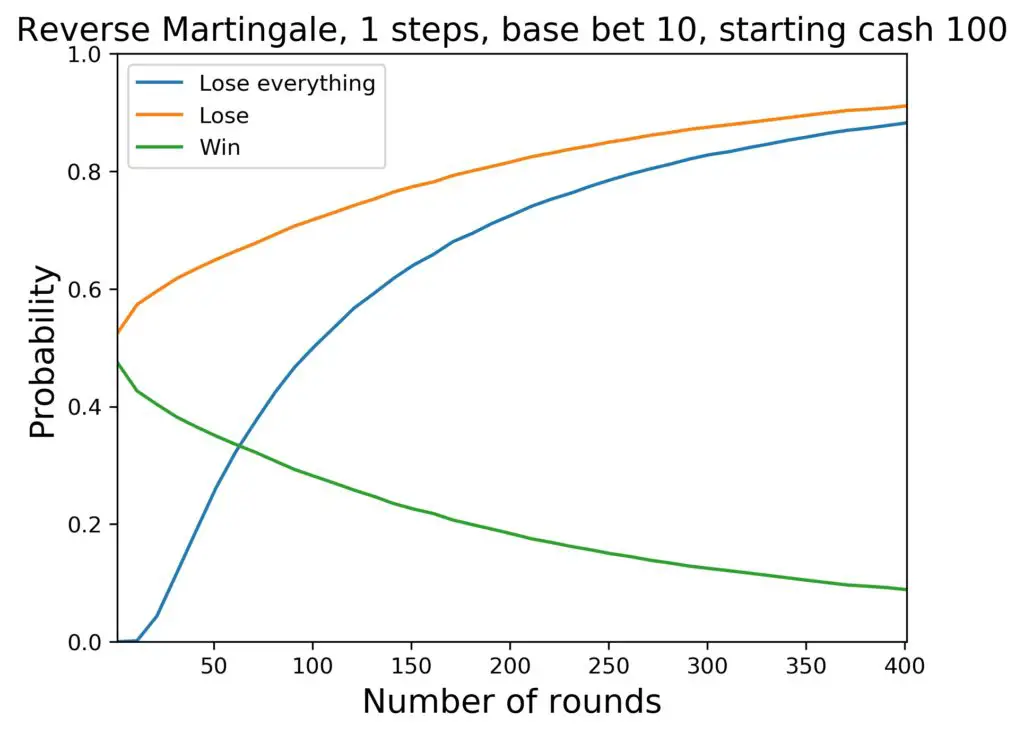
Here are the key data of interest again for this run (amount and percentages are rounded):
- the average cash at hand after 400 rounds is 22 $.
- the probability for a total loss is 88 percent
- the probability for a loss is 91 percent
- the probability for a win is 9 percent
To get a better feel for what happens after shorter amounts of time, here is the plot with the corresponding numbers again, but only up to 40 rounds:
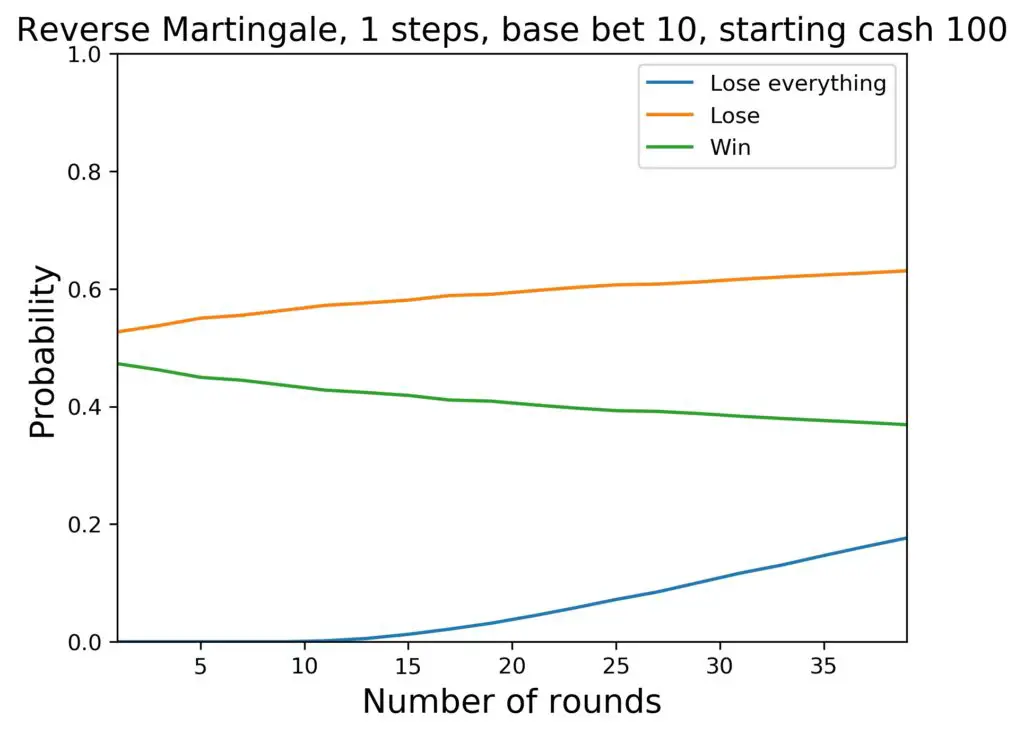
Here are the key data of interest again for this run (amount and percentages are rounded):
- the average cash at hand after 40 rounds is 80 $.
- the probability for a total loss is 18 percent
- the probability for a loss is 63 percent
- the probability for a win is 37 percent
So that is what you can expect by playing Roulette, betting on red, black, even or odd, and betting the same amount all the time.
Dependence of Probabilities for the Reverse Martingale Strategy in Roulette on the Amount of Cash in the Beginning
I would say that his dependence is accessible to our instincts. The less we start with, the lower our probability of winning gets, right? Let us check that assumption. We go back to 4 steps in the progression and 100 $ starting cash. Then, we lower the starting amount of cash such that we get to the same steps as above, and finally arrive at the base amount:

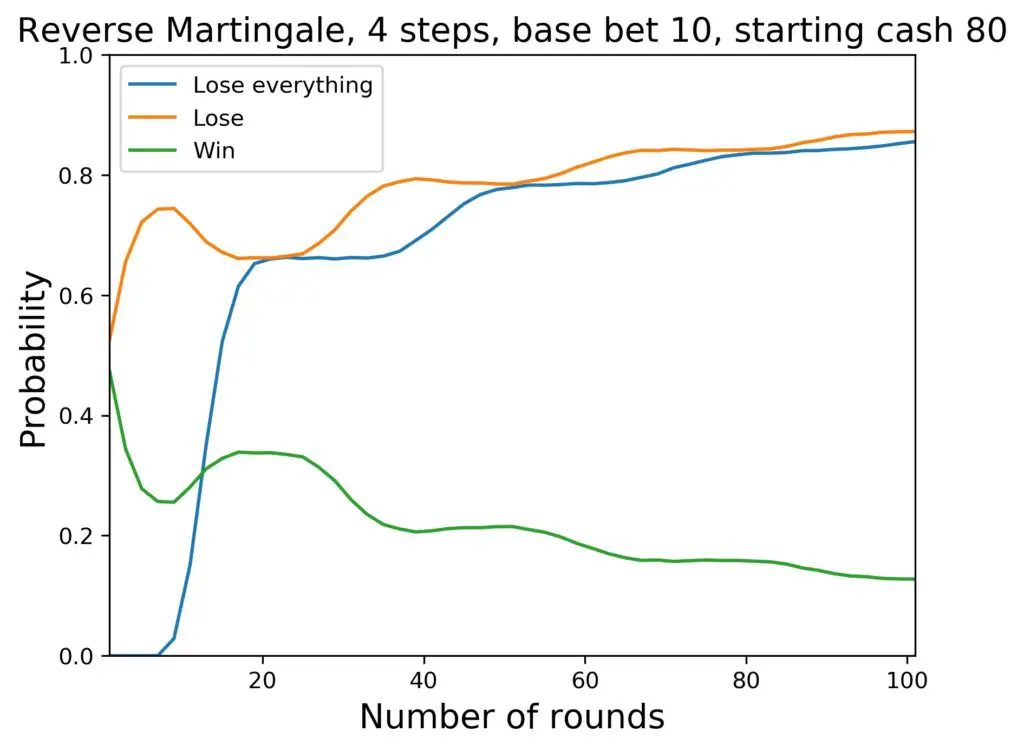

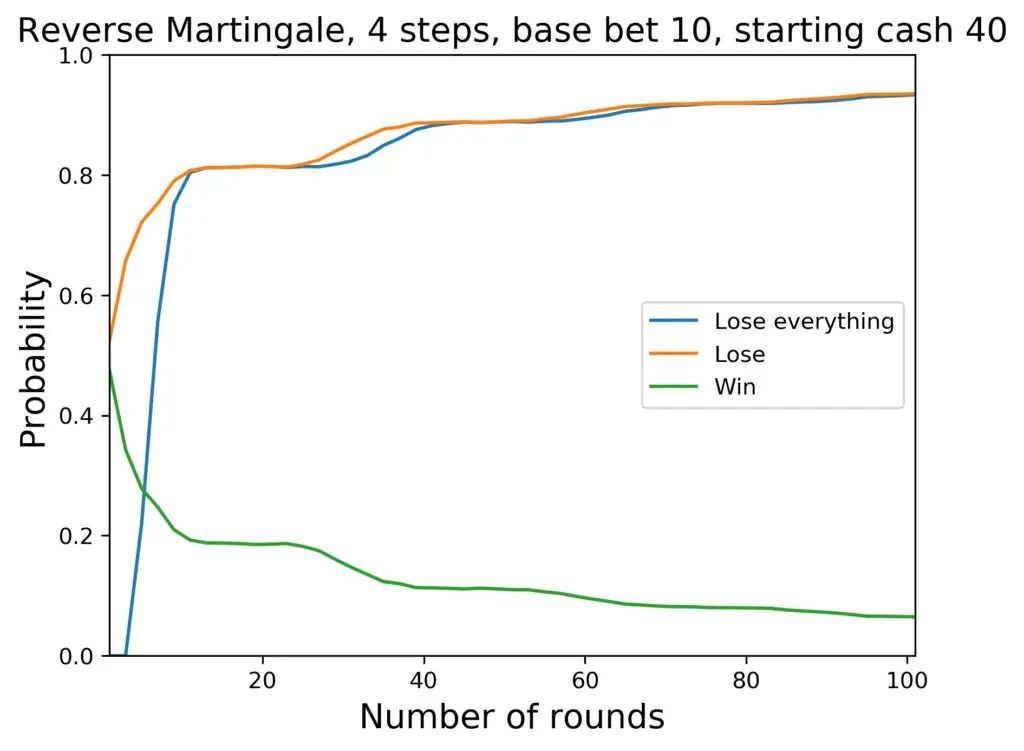
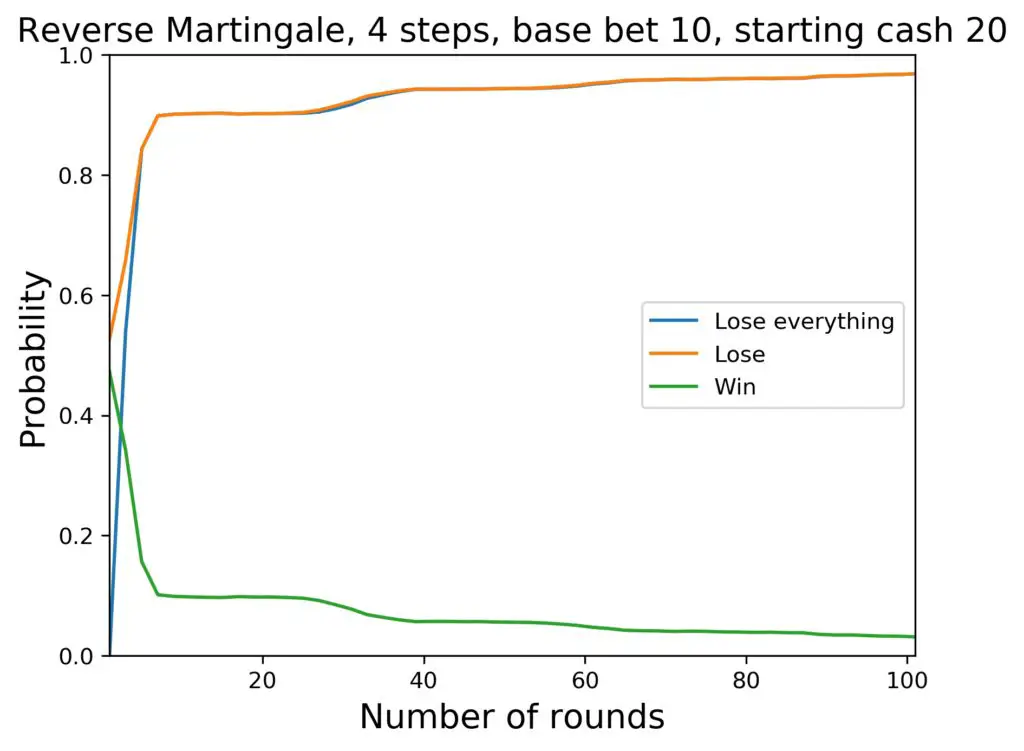
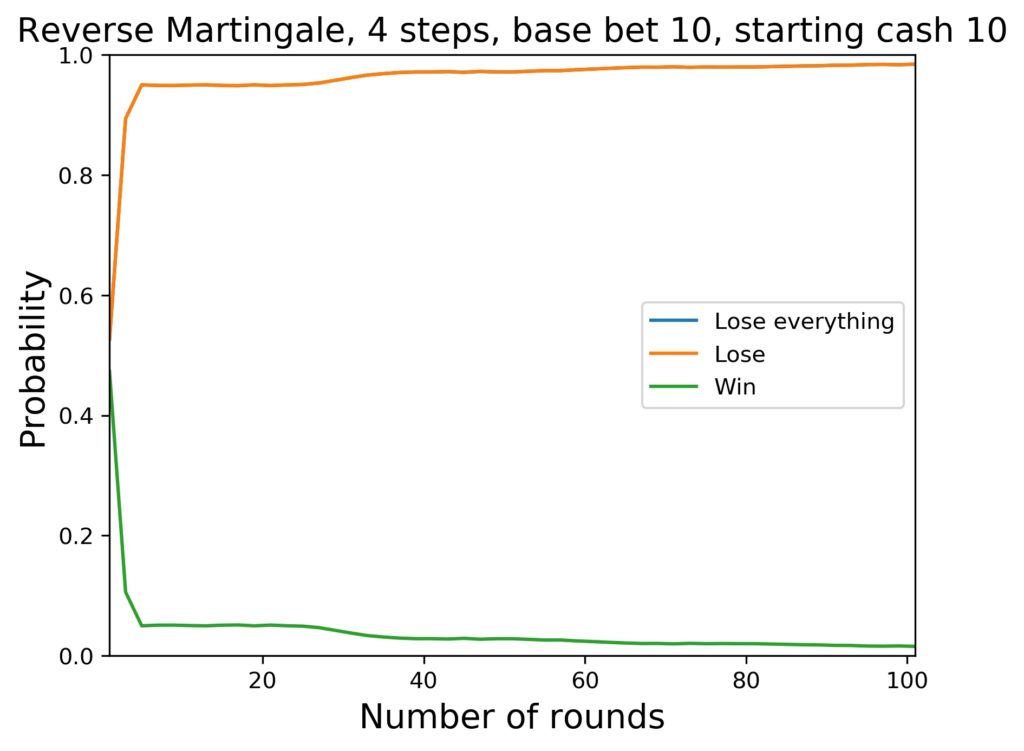
We can see how the probabilities change. The average cash goes as follows:
- Starting at 100 $ after 100 rounds: 56 $
- Starting at 80 $ after 100 rounds: 44 $
- Starting at 60 $ after 100 rounds: 32 $
- Starting at 40 $ after 100 rounds: 21 $
- Starting at 20 $ after 100 rounds: 10 $
- Starting at 10 $ after 100 rounds: 5 $
What do we take away from this? Maybe the following observations:
- The average amount of cash remaining is roughly half the starting amount, plus a bit more.
- More cash in the beginning means more time to get a big win, thus a higher winning probability and a higher amount of cash compared to the starting amount.
- The probability of getting a long-term run and win with just the base amount is one and a half percent only (for four progression steps).
Overall, this isn’t very convincing. The system can be used with a low starting budget, but the chances for success are not particularly high.
Strengths and Weaknesses of the Reverse Martingale System for Roulette
The Reverse Martingale system for Roulette has a couple of strengths and weaknesses that we can formulate. Referring to the title of this article, the system is certainly not genius. However, it isn’t really a disaster, either. Here are my summary lists:
Strengths of the Reverse Martingale System for Roulette
- The player can use the system with a starting amount of cash that can be as low as the just the base amount. This is an advantage in particular compared to the Martingale system.
- The player is forced (at least in theory) to choose a fixed number of steps that they want to go to at most in the progression system. This can be used with a risky playing style (higher number of steps) or a conservative one (lower number of steps).
- The average cash in hand after a larger number of rounds at the Roulette table is actually greater than for betting the same amount all the time, i.e. more or less not using a betting system.
- The system does not suffer from existing table limits, unless taken to very risky extremes.
Weaknesses of the Reverse Martingale System for Roulette
- While possible wins are high, the probabilities to get a big win are very low.
- There is no decisive advantage in terms of the winning probability at any point, neither in the short term, nor the long term.
What I mean by the latter statement will become clear to you, once you read my article Odds in the Martingale System: Math and Excel Cheat Sheet. There you will see an example of a decisive advantage of a betting system for the player, at least in winning probability.
In-Depth Analysis of the Martingale System for Roulette
While the Reverse Martingale System is known among players of all sorts of games of chance, the Martingale System is famous. It is probably the one system that most players want to know about. There is a lot to know about it, too.
I have taken the time to take it apart and simulate the Martingale System in even greater detail than the Reverse Martingale System in the article you just read. Take a look at both analyses and decide which one you would trust more with your hard-earned money.
Speaking of hard-earned money, please be sure to read my simulation disclaimer, if you haven’t already.

