Does the James Bond Roulette strategy actually work? Or does it just amount to losing at Roulette, but with style? I simulated and analyzed a lot of Roulette strategies recently, and here is the verdict for 007’s preferred system:
In short, the James Bond Roulette strategy is a combination bet. As such, it works just as well as any of the simple bets it consists of, when it comes to the average expected profit per round, which is the house edge.
But wait, how does this work in detail? Glad you asked. Read on, and I’ll show you every detail you need to know. And by the way, don’t expect any secret (and maybe illegal) gadgets or tricks to beat the system, because such things do not exist. What you can expect, though, is a takeaway that you have most probably never heard before.
The James Bond Roulette Strategy Explained in a Nutshell
James Bond
is a world famous character from the original works of British author Ian Fleming. Most of us know James Bond and his well-known code numbe 007 from the quite numerous Movies made over the years. One particular kind of place, where the character of James Bond meets people, “does business”, and faces off his opponents, is a casino.
So it isn’t a huge surprise that there is a Roulette strategy named after James Bond. Roulette is a rather well-known game of chance and allows for several different ways to place a bet. So what exactly is the James Bond Roulette strategy?
The James Bond Roulette strategy is a combination bet, where a total amount of usually 200 $ is distributed to three bets as follows: 140 $ on the high numbers (19 to 36), 50 $ on a Six Line or Double Street (the numbers 13 to 18), and 10 $ on the Single number 0.
The usual expectation that players have with this kind of bet is that the combination of the parts covers more possible outcomes, thus somehow reducing the risk of a loss. However, the amount of uncovered numbers is not the important point to consider.
It is more important to calculate the average expected profit, and we’ll do that in just a minute. Before that, we need to clarify a few more things.
The James Bond Roulette Strategy for European and American Roulette
You already noticed it – one part of the James Bond Roulette Strategy, as it is described, is to put a single bet on the number 0. This is actually the case only for the European variant of Roulette, where there are the numbers from 1 to 36 on the Roulette wheel, plus the 0. In total, there are 37 numbers on a European Roulette wheel.
In American Roulette, there is an additional number, 00, which increases the total numbers on the Roulette wheel to 38. In this case, the Single bet on 0 (European variant) can be replaced by a Split bet on 0 and 00. But that doesn’t really matter, as you’ll soon discover.
Does the James Bond Roulette Strategy Work?
The James Bond Roulette strategy works exactly as well as any simple bet at the Roulette table. This can be understood by comparing the expected average profits for any simple bet with the combined bets of the James Bond strategy, which results in the usual house edge.
In order to understand this, we’ll go through two steps in the following two sections. First, we will look at the odds, payouts, and profits for the individual types of bets that are combined in the James Bond strategy.
After that, we will use the profits and probabilities for those individual bets to compute the resulting expected average profit for the James Bond Roulette strategy. This will probably be the biggest eye-opener of this entire article, so stay with me, ok?
Odds of Winning With the James Bond Roulette Strategy
The odds of winning with the James Bond Roulette strategy are combined from the individual odds for each bet in the strategy, and the expected profit computes to exactly the house edge. Thus, the James Bond Roulette strategy does not provide any advantage or disadvantage compared to a simple bet at the Roulette table in terms of expected profit per round.
Let us look at the details of this rather unintuitive statement. Putting together the individual bets from the above example, we have the following situation (sticking with European Roulette for clarity, but it really doesn’t matter):
- A total amount of 200 $ is distributed on three non-overlapping (that seems important, but not even this part is essential) bets on:
- the Higher numbers from 19 to 36, on which we bet 140 $
- the Six Line of numbers from 13 to 18, on which we bet 50 $
- the Single number 0, on which we bet 10 $
Next, we need the probabilities for a win or a loss for these three different bets. Furthermore, we’ll compute the profit in each case and discuss what happens in case of a loss, when that happens, and how probable that is. For the individual bets comprising the James Bond Roulette strategy, we get:
| Bet | High Numbers (19 - 36) | Six Line (13 - 18) | Single (0) |
|---|---|---|---|
| Amount placed on bet | 140 $ | 50 $ | 10 $ |
| Probability of winning with this bet (European) | 18/37 = 48.6 % | 6/37 = 16.2 % | 1/ 37 = 2.7 % |
| Odds for this bet | 18 : 19 | 6 : 31 | 1 : 36 |
| Payout for this bet | 1 : 1 | 5 : 1 | 35 : 1 |
| Profit for this bet alone in case of a win | 140 $ | 250 $ | 350 $ |
| Average expected profit for this bet alone (defines the house edge) | -3.78 $ = -2.7 % | -1.35 $ = -2.7 % | -0.27 $ = -2.7 % |
| Profit for this bet in case of a win, considering the total bet of 200 $ | 80 $ | 100 $ | 160 $ |
The numbers in the table mean the following:
- Amount placed on bet: the amount of money placed on this type of bet in the James Bond Roulette strategy. In our example, the three amounts add up to 200 $.
- Probability of winning with this bet (European): the winning probability of this particular individual bet in European Roulette (with 37 numbers on the Roulette wheel). This number is given both as a fraction and a percentage.
- Odds for this bet: the odds for this individual bet, which is written as the number of positive outcomes for the player to the number of negative outcomes.
- Payout for this bet: the payout for this individual bet, given as the number of times the bet will be paid out to the player in addition to getting the bet back. Example: 5 : 1 means the player bets one dollar, wins 5 dollars in addition, and has 6 dollars after the round instead of the 1 dollar before the round.
- Profit for this bet alone in case of a win: what the player has more than before playing this bet in case of a win. Computed by multiplying the bet with the payout.
- Average expected profit for this bet alone (defines the house edge): the amount of money lost per round on average, when playing this bet with the given amount. The house edge is given in parentheses and in percent. Notice that the percentage is the same for all bets used in the James Bond Roulette strategy. I’ll explain this one in detail in the following section.
- Profit for this bet in case of a win, considering the total bet of 200 $: this is for reference and the computation in the next section. Since the total bet in the combination of our strategy is 200 $ (in our example), the profit of an individual win is cut by the other two bets that are lost at the same time. So for these numbers in the columns, subtract the other two bets from the individual profit of the winning bet, and you will arrive at each number given.
With the numbers in this table, you can perfectly see what happens in case of a win with the James Bond Roulette strategy for each type of bet individually. However, we need to understand what happens in combination of these three bets in order to understand if and how the James Bond Roulette strategy works.
In order to do this, we compute the expected value for the average profit after one round of playing the James Bond Roulette strategy. This is explained in detail in the following section.
Understanding the Expectation Value for the Profit With the James Bond Roulette Strategy
The expected average profit after one round of playing the James Bond Roulette strategy is computed from the profits and winning probabilities of the individual bets in the strategy. But how do we do this?
Before we combine bets, let us compute the expected values that you saw in the table above for each individual bet separately first. These will give us simpler examples, which are interesting at the same time. What we need to do is to sum all (exclusive, i.e., non-overlapping) possibilities, more precisely their profit times the probability of their occurrence.
Since the individual bets themselves are non-overlapping in this case (i.e., a number does not belong to the Six Line we use and the High Numbers at the same time), we can simply sum over the three individual bets. But a more general situation is also possible for overlapping individual bets, which doesn’t change the outcome, just the way to get there (see below).
For the bet on the high numbers (19 – 36), the probability of winning is 18/37, the probability of losing is 19/37 (we stick to European Roulette again, because this computation works exactly in the same way for American Roulette, where the number of possible outcomes is 38 instead of 37).
If we bet an amount of a dollars, the expected average profit after one round is a (the profit for a win) times the winning probability, plus -a (the profit for a loss) times the losing probability. I use the variable a to make the following clear in the calculation:
- The resulting expected average profit is proportional to the bet.
- Thus, the resulting expected average profit can indeed be best written and understood as a percentage of the bet.
- The mechanism that leads to the result is similar in all cases that we will look at here, and the use of a variable for the bet helps to make that clear in particular.
The Expected Average Profit for a Bet on the High Numbers in European Roulette
So, here we go. The average expected profit for a bet on the high numbers in European Roulette is
\[ a \frac{18}{37} + (-a)\frac{19}{37} \]
Now, when I compute this, I’ll leave the fractions there as long as possible and I’ll separate the bet variable a from the rest. This will help you understand, where the similarity in all these calculations comes from:
\[ a \frac{18}{37} + (-a)\frac{19}{37} = a \left( \frac{18}{37} – \frac{19}{37} \right) = a \frac{18 – 19}{37} = a \frac{-1}{37} \]
How much is 1, divided by 37? That’s roughly 0.027. So the average expected profit for the bet on the high numbers is -2.7 % of the bet. If you are somewhat familiar with the math of Roulette, you’ll recognize this number: it is the house edge for European Roulette.
The Expected Average Profit for a Bet on a Six Line in European Roulette
Ok, on to the next one, the Six Line. Betting on the numbers from 13 to 18, the probability of winning is 6/37, the probability of losing is 31/37. What do these numbers lead to in terms of the average expected profit after one round?
Here, if we bet an amount of a dollars, the expected average profit after one round is 5 a (the profit for a win) times the winning probability, plus -a (the profit for a loss) times the losing probability:
\[ 5 a \frac{6}{37} + (-a)\frac{31}{37} \]
Calculating this, I’ll combine the fractions again and take the a out:
\[ 5 a \frac{6}{37} + (-a)\frac{31}{37} = a \left( \frac{30}{37} – \frac{31}{37} \right) = a \frac{30 -31}{37} = a \frac{-1}{37} \]
That’s the same result as before, and it happens in much the same way, too, if we write it down like this. So now, we have the justifiable suspicion that the third case (the Single bet) will produce the same result, don’t we? Let’s find out.
The Expected Average Profit for a Bet on a Single Number in European Roulette
Betting on a Single number, in our case on 0, the probability of winning is 1/37, the probability of losing is 36/37. What do these numbers lead to in terms of the average expected profit after one round?
Here, if we bet an amount of a dollars, the expected average profit after one round is 35 a (the profit for a win) times the winning probability, plus -a (the profit for a loss) times the losing probability:
\[ 35 a \frac{6}{37} + (-a)\frac{36}{37} \]
Calculating this in the same way as before, we get
\[ 35 a \frac{1}{37} + (-a)\frac{36}{37} = a \left( \frac{35}{37} – \frac{36}{37} \right) = a \frac{35 -36}{37} = a \frac{-1}{37} \]
And, indeed, the result is the same again. So, with these calculations under our belt, we are ready to do the one we came here for: the James Bond Roulette strategy.
The Expected Average Profit for a Bet with the James Bond Strategy in European Roulette
The only difference to a simple bet here is that there are three different possibilities to win, and one to lose. These depend on the number that the ball lands on in the Roulette wheel, and they are:
- The ball lands on zero: the Single bet wins. Probability 1/37.
- The ball lands on a number from 1 to 12: the player loses. Probability 12/37.
- The ball lands on a number from 13 to 18: the Six Line wins. Probability 6/37.
- The ball lands on a number from 19 to 36: the High Numbers win. Probability 18/37.
So far, so good, but what about the profits we need to use in the calculation? I’ll write down the same calculation twice: the first time with our example numbers, and the second time with variables. In this way, we can use the numbers from our example table above for the first calculation. The expected average profit after one round becomes:
\[ 160 \frac{1}{37} + (-200) \frac{12}{37} + 100 \frac{6}{37} + 80 \frac{18}{37}\]
This is the sum we need to calculate. The order of the terms is just the order of the numbers on the Roulette table, but is arbitrary for the sum. The result, computed by taking out the common factor of 1/37, is
\[ \frac{1}{37} (160 \cdot 1 – 200 \cdot 12 + 100 \cdot 6 + 80 \cdot 18) = \frac{1}{37} (160 – 2400 + 600 + 1440) = \frac{1}{37} (-200) = 200 \frac{-1}{37} \]
In the last step, I rewrote the expression slightly to prepare you for what is coming. Yes, indeed, this is the same result again. Keep in mind that the bet was replaced earlier by the variable a. If we did this now, after the calculation is done, we would replace 200 by a, and there would be our familiar result of the house edge. But I wouldn’t believe that, either, without proof. So I’ll give you the proof:
Derivation of the Expected Average Profit for a Bet with the James Bond Strategy in European Roulette
The easiest way to write this with variables is by splitting the variable a up into three parts \( a_1 \), \( a_2 \), and \( a_3 \) such that that their sum is
\[ a_1 + a_2 + a_3 = a \]
And that is all we have to do. I know what you are going to say right here and right now: hey, wait! Don’t we have to set up the ratios between these three parts correctly in order to make the system work? The answer is no, and that comes as a surprise to many. You’ll see in a minute or two, how the ratios are not important at all: we’ll set up the general calculation, and the ratios will disappear from the final result.
So what the new variables \( a_1 \), \( a_2 \), and \( a_3 \) are there to replace are the bets on the individual parts of the James Bond Roulette strategy. Concretely, we just go back to the previous sum of probabilities times profits, and replace the numbers accordingly. We had:
\[ 160 \frac{1}{37} + (-200) \frac{12}{37} + 100 \frac{6}{37} + 80 \frac{18}{37} \]
It is pretty clear, that -a has to replace the (-200) in this sum, because for a loss, we just lose the entire bet. In the other cases, however, we need to calculate the profit for each of the individual bets in terms of \( a_1 \), \( a_2 \), and \( a_3 \), considering that when one of them wins, the other two lose at the same time.
So, what is the profit for the Single bet, for example? Let’s use the variable \( a_1 \) for the Single bet portion, i.e. \( a_1 = 10 \) (I’ll just drop the dollar signs for the moment). Then, if the single bet wins, we win 35 times \( a_1 \). At the same time, \( a_2 \) and \( a_3 \) are lost. Thus, the profit \( p_1 \) for the Single bet in terms of \( a_1 \), \( a_2 \), and \( a_3 \) is:
\[ p_1 = 35 a_1 – a_2 – a_3 \]
A quick check with our numbers in the table and example shows that this gives us our example profit for the Single bet:
\[35 \cdot 10 – 50 – 140 = 160 \]
Now, for the Six Line bet, we use the bet portion \( a_2 \). Adjusting the previous formula to give us the profit \( p_2 \) for the Six Line bet in terms of \( a_1 \), \( a_2 \), and \( a_3 \) is:
\[ p_2 = 5 a_2 – a_1 – a_3 \]
This can be quickly checked with our example numbers as well, giving us
\[5 \cdot 50 – 10 – 140 = 100 \]
And, finally, for the High numbers bet, we use the bet portion \( a_3 \), adjust the previous formula, and get the profit \( p_3 \) for the High numbers bet in terms of \( a_1 \), \( a_2 \), and \( a_3 \) as:
\[ p_3 = a_3 – a_1 – a_2 \]
which quickly checks out as well to be
\[ 140 – 10 – 50 = 80 \;. \]
Now that we have the profits all set up and checked, we are ready to calculate the average expected profit for the combined bet in the James Bond Roulette strategy:
\[ p_1 \frac{1}{37} + (-a) \frac{12}{37} + p_2 \frac{6}{37} + p_3 \frac{18}{37} \]
Inserting the profits as defined above, we get
\[ (35 a_1 – a_2 – a_3) \frac{1}{37} + (-a) \frac{12}{37} + (5 a_2 – a_1 – a_3) \frac{6}{37} + (a_3 – a_1 – a_2) \frac{18}{37} \]
Now, all we have to do is simplify this. Once again, I’ll take out the overall factor of 1/37 and write all the other terms in one large pair of parentheses:
\[ \frac{1}{37}\left((35 a_1 – a_2 – a_3) + (-a) 12 + (5 a_2 – a_1 – a_3) 6 + (a_3 – a_1 – a_2) 18 \right) \]
Multiplying factors together, we arrive at
\[ \frac{1}{37}\left(35 a_1 – a_2 – a_3 – 12 a + 30 a_2 – 6 a_1 – 6 a_3 + 18 a_3 – 18 a_1 – 18 a_2 \right) \]
Next, we sum up all terms with the same variables in the parentheses, which yields
\[ \frac{1}{37} \left(11 a_1 + 11 a_2 + 11 a_3 – 12 a \right) = \frac{1}{37} \left(11 (a_1 + a_2 + a_3) – 12 a \right) \]
In the last step, I took a common factor of 11 out of the sum of the \( a_i \). What we notice now is that we can replace the sum via \( a_1 + a_2 + a_3 = a \), and as a result, none of the individual portions remain in the formula. Instead, we just have
\[ \frac{1}{37} \left(11 a – 12 a \right) = – a \frac{1}{37} = a \frac{-1}{37} \]
And that is the result that I promised you, as surprising as it may be. It really doesn’t matter, how you distribute your money on the individual parts of the James Bond Roulette strategy: it works exactly in the same way, not depending on the individual amounts.
Of course, this pertains to the expected average profit per round. More precisely, it just tells you that you will lose exactly the same amount of money on average each round with the James Bond Roulette strategy as with a simple bet, and that is 2.7 percent of the total bet. Actual wins and losses for the individual rounds may vary greatly – this general statement regards only the average.
The James Bond Roulette Strategy is Just a Combination Bet
In the previous section I showed you how to calculate the expected average profit per round in the James Bond Roulette strategy. Towards the end of that section, it became clear that there is a general principle that underlies this construction and enables us to compute this sort of profit for any combination bet.
In fact, what we have learned is that the James Bond Roulette strategy is just a combination bet. What we have also learned ist that the precise splitting of the total bet into the individual amounts does not matter at all for the expected average profit, which always comes out to be the house edge. This leads to startling possibilities that I will discuss below in the section on modifications to the James Bond Roulette strategy.
In fact, this is a general property of combination bets: since the house edge is the same for all individual events or bets, you can combine them any way you like and with any amounts you think are cool to use, and the resulting average expected profit will always be the same. Still not convinced? Read more about this fact in my article Why All Roulette Combination Bets Are the Same.
Now that we know this, is there anything else we can do to improve our chances?
Combining the James Bond Roulette Strategy With the Martingale System
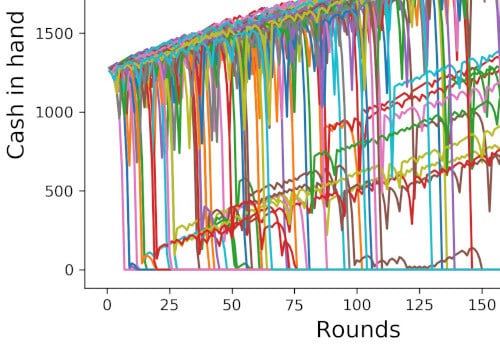
What I often saw when I researched the James Bond Roulette strategy is that it is sometimes combined with the Martingale betting system. This is an attractive idea, because it offers a higher-than average winning probability over the first couple of rounds in the Martingale progression, as I have discussed in detail in my article Odds in the Martingale System: Math and Excel Cheat Sheet.
But before you jump on this hint of a system that beats the house edge (which doesn’t exist), let me add this: while the probability for a loss in the first rounds of a Martingale progression is substantially lower than the probability for a win, this doesn’t take into account, how big a loss or win we are talking about.
The important thing to realize is that the average loss in the Martingale system is much bigger in size (downward) than the average win, and the house edge remains exactly. You’ll find all the details in the article that I just mentioned. But I have even more to show you what the Martingale system does in Roulette. Check out my article Martingale Roulette Strategy: Full Outcome Analysis with Charts.
Is the James Bond Roulette Strategy Legal?
The James Bond Roulette Strategy is perfectly legal, as long as it doesn’t violate any of the casino’s rules. More precisely, any kind of strategy that involves combining legal bets within the table limits is legal in a casino.
The rules valid in a particular casino are made available to the players to begin with. Furthermore, there are usually regulations in place, that governing bodies issue for casinos and gambling in general. Particular orders of bets, their combinations, or bet-increasing progressions don’t tend to fall in this domain.
Limits of the James Bond Roulette Strategy
While playing the James Bond Roulette strategy is not illegal, the use of the strategy in a casino is certainly limited. The main reason is the existence of table limits. To be more precise, there are lower and upper limits on the size of bets that can be placed on inside and outside bets at a Roulette table.
What the size of these limits are is noted somewhere at the Roulette table so that the players can see and understand the limits. Typical table minima are in the range of 1 $ to 10 $. Typical table maxima can be as low as 150 $, and more typically 1000 $, depending on the type of bet (outside or inside).
The reason, why it matters for the James Bond strategy, is that for the usual 200 $ example, the bets are pretty sizable: 140 $, 50 $, and 10 $. If you would combine this with a Martingale system, as discussed above, you can reach the table limit quite quickly, in particular, because there also limits on combined bets by a single player.
Doubling up the amount of 200 $ only three times will bring us to 1600 $, which might be unfeasible, if it cracks the table limits. So any James Bond, who would like to use the Martingale system, should keep this in mind and adjust the starting bet down accordingly.
Is There a Modified James Bond Roulette Strategy?
Some people and websites suggest that you can modify the James Bond Roulette strategy to make it better/win more/whatever. By now, you already know better. After reading this article, you have learned that changing the parts in a combination bet does not change anything, in particular about the average profit per round.
On the other hand, this rule also tells you, how you can modify the James Bond Roulette strategy, and still have the same chances (basically like everybody else). Read more on why exactly the following are true in my article Why All Roulette Combination Bets Are the Same. So what are the modifications that you can make?
- Change the type of bet used: use red versus black or even versus odd instead of the high numbers. Yes, the number of covered versus uncovered numbers changes, but that doesn’t matter.
- Add more individual bets to the mix: you can combine two Street bets instead of using a Six Line, for example. It doesn’t matter what the number of individual bets in the combination is: three, four, two, whatever.
- Cover 0 and 00 with a Split bet in American Roulette: you can choose to do this, cover 0 only with a Single, cover 00 only with a Single, or don’t cover the green numbers at all. Doesn’t matter.
- Change the size of the individual bets as you like: we have seen that the individual bet sizes \( a_1\), \(a_2\), and \(a_3\) do not appear in the final result for the average expected profit per round. So, as long as you keep the sum constant at your desired amount, you can choose these totally freely.
The last point in this list of possible modifications warrants an example. And it’s a fun one, too.
Play the James Bond Roulette Strategy Like a Boss
What would you say, if I told you to swap the bet sizes for the Single on 0 and the High numbers on 19 – 36? More precisely, bet the 140 $ in our example on 0, and the 10 $ on 19 – 36? Sounds crazy?
Yes, it certainly does, but it doesn’t change the average expected profit per round. Here is the calculation. First, remember the probabilities:
- The ball lands on zero: the Single bet wins. Probability 1/37.
- The ball lands on a number from 1 to 12: the player loses. Probability 12/37.
- The ball lands on a number from 13 to 18: the Six Line wins. Probability 6/37.
- The ball lands on a number from 19 to 36: the High Numbers win. Probability 18/37.
While the probabilities stay the same, we need to calculate the profits for our new betting setup. So the idea is that we bet our total of 200 $ on three individual bets as follows: 140 $ on the Single number 0. 50 $ on the Six Line 13 – 18. And finally, 10 $ on the High number 19 – 36. Here are the corresponding profits:
- For the Single bet on 0 we have a profit of 35 times 140 $, minus the other two, 10 $ and 50 $. That results in a whopping 4840 $.
- For the Six Line on 13 – 18 we have the same profit as before, 5 times 50 $, minus the other two, 10 $ and 140 $, which results in 100 $.
- For the High numbers 19 – 36 we have a profit of 10 $, minus the other two, 140 $ and 50 $, which results in -180 $.
- For the numbers 1 – 12, which is a loss of all bets, we have the profit of -200 $, same as before.
Now we add all these up, multiplied with their probabilities, and get
\[ 4840 \frac{1}{37} + (-200) \frac{12}{37} + 100 \frac{6}{37} + (-180) \frac{18}{37}\]
And, taking out the factor of 1/37 again, we get the following sum (as always):
\[ \frac{1}{37} ( 4840 – 2400 + 600 – 3240 ) = \frac{1}{37} ( -200 ) = 200 \frac{-1}{37} \]
Still, however tempting all that may sound to you to use, the bottom line from all this should be made clear once again: both on average and in the end you’ll lose your money, if you play a game of chance in a casino.
More Different Roulette Strategies
The quest for a strategy that will improve the player’s chances of winning at the Roulette table is truly fascinating. Creative beings, as we humans are, like to explore and try different things to solve difficult problems. And if we want something really badly, we don’t give up easily.
However, Roulette, in particular in a casino, is an interesting challenge. The point is that the rules of probability work for the casino on average. While most players try to beat the system, that is not possible (in the sense that you cannot reliably win every time).
All the player can do is try to find ways to maximize certain probabilities, which is what I investigate in my reviews and analyses of the various betting systems in Roulette. Check out my article Martingale Roulette Strategy: Full Outcome Analysis with Charts for the most promising bump in probability that I have seen so far.
