
In our family, we love to play board games with our kids. And the kids love it, too. In particular, they like games that make them think a bit about strategy and what happens, plus are fun at the same time. For me as a geeky dad, a game that has some non-trivial aspects to it adds a bonus by making me ask non-obvious questions (which entertains me). So, what is my take on Unicorn Glitterluck: Cloud Crystals?
Unicorn Glitterluck: Cloud Crystals is a board game for 2 to 4 players ages 3 and up. The game material is of excellent quality. The game outcome is mainly determined by rolling dice, but the game remains interesting and fun until the end and has several educational aspects. I highly recommend it.
But that is just my quick take on the game. There are quite a number of things about it that deserve to be shared in more detail, so here we go:
The Idea behind Unicorn Glitterluck: Cloud Crystals
In the board game Unicorn Glitterluck: Cloud Crystals, 2 to 4 players race across the clouds, when they are trying to get away from the rain and into the sunshine. But do they just race? No, they are collecting crystals along the way! And that is what really counts, as I’ll explain below, where I talk about what wins the game.
What’s in the Box

The game box contains:
- the game board (picture below), which is assembled from three large puzzle pieces
- four wooden unicorn
 figures (see pictures above and below) with different colors (and names)
figures (see pictures above and below) with different colors (and names) - two dice
 (pictures below), a blue one with clouds, and a pink one with crystals
(pictures below), a blue one with clouds, and a pink one with crystals - a bag with 60 pink plastic crystals (this picture)
- the game instructions and rule book (link to the pdf below)
The material (board, figures, crystals) are of high quality. In particular:
- although it is assembled from three pieces every time, the board is stable and can take frequent handling by children well
- the wooden unicorns have the perfect weight for playing. They also allow for creative play outside the rule book, like stacking or similar ideas.
- the crystals have a nice design. In particular, I like the shape, because the crystals appear different easily (by lying on various different surface parts), although they all are exactly the same.

Unicorn Glitterluck: Cloud Crystals – The Rules
I find the rules of the game simple enough for 3-year-olds to follow, but complex enough to make the game interesting and entertaining even for adults. Here are the details.
The Game Board of Unicorn Glitterluck: Cloud Crystals

The game board features the dark starting cloud in the upper left corner, the white finishing cloud in the lower right corner, and in between those a number of white clouds, pink clouds with a die on them, and purple clouds with a present on them. In addition, there are three rainbows that each connect two of the clouds.
Dice and Game Mechanics
The game is played by rolling dice: the players take turns rolling the blue die, which features little clouds instead of the standard dots. If a player’s unicorn moves to a pink cloud, they are allowed to roll the pink die, which features little crystals instead of dots.

The blue cloud die has one side with the maximum of three clouds, two sides with two clouds, two sides with one cloud, and one side with the image of a muffin. The number of clouds tells the player, how many clouds their unicorn may advance on the board towards the white finish cloud. If they roll a muffin, however, the unicorn stays put (and eats the muffin), so that corresponds to a value of zero on the die. In terms of probabilities, it is twice as likely to roll a 1 or a 2 than it is to roll a 3 or a 0.
The fact that the number of clouds is limited to a maximum of three, and includes a zero, makes for a good pace of gameplay. Since it takes 26 steps to arrive at the finish cloud, having a six on this die would certainly speed up the game too much and leave much of the potential (collecting crystals) untapped.

The pink crystal die has one side with three crystals, two sides with two crystals, and three sides with one crystal. A player will roll the pink die when arriving on a pink cloud on the board, and collect the number of crystals shown on the die. These crystals are added to the player’s pile, which is the actual score in the game (see below).
From the distribution of crystals on the die it is clear that it is most likely to collect one crystal, and that collecting three crystals at a time doesn’t happen that often. Still, it is important that the crystal count is increased every time a player lands on one of the pink clouds.
Special Moves and Events
There are a couple of noteworthy special events and circumstances in the game. You can see the board-related ones in the picture above.
Rainbows: These serve as one-way slides. A unicorn landing on the cloud at the beginning of the rainbow at the end of a move must slide to the cloud at the end of the rainbow. And it must make a happy noise and jump over the ladybug, according to my daughter.

Presents: A player who arrives on one of these clouds is allowed to (actually has to) give one crystal to one of the other players (and gets to choose to which one of the others). The crystal comes from the reservoir of crystals, not from their own pile, so that is actually something very nice to do.
Finish Bonus: The first unicorn to arrive at the finish gets to collect four bonus crystals that lie there waiting.
Sharing Clouds: Two or more unicorns can share the cloud on which they are. Nobody has to go back to the start for any reason in the game.
Game Objective and Winning the Game
The game objective is to collect as many crystals as possible. The winner is the player, who has collected the most crystals among all players right after the time/move when the first unicorn arrives on the white finish cloud and collects the four bonus crystals there.
So, the first finisher is not always the winner. While it does help to collect the four bonus crystals for finishing, it is much more important to be successful in collecting crystals as often and as numerous as possible during the entire game. The question how likely it is that the finishing unicorn does not win was the initial push for me towards wanting to run a Monte-Carlo simulation of this game. If you are interested in the answer to this question and other statistics about what can happen, make sure to check out my analysis below.
Great Idea: Determining the Winner Without Counting
There is one other nice thing about this game that I want to share, which is an easy way to determine the winner, even without being able to count. This can be helpful for very young kids playing as well as for other ideas about helping kids learn to count.
On the back of the game board, there are four lines of clouds, one for each unicorn. The figures are placed in their spots, and the crystals collected are laid out in front of each of them, as I show in the picture. This makes the winner obvious and provides ample opportunity for additional counting games and other ideas.

My Favorite Aspects of the Game
There is a main reason why I write this review: I personally found a fair amount of intellectual stimulation when I started playing this game and thinking about all the possible outcomes, etc. But that isn’t all, I also like a few other things in particular. Here they are.
The First Finisher is not Automatically the Winner
This aspect is just genius. It helps keep everyone engaged by not losing hope just because they seem to always be rolling low cloud numbers. It also makes the kids constantly keeping scores in their heads trying to figure out who is in the lead (because the obvious position on the board is only part of the equation).
The Present Clouds
These points in the game allow for moments of kindness, but also for discussing options, like who needs help the most, etc. A very nice touch to the game.
Having Fun with Muffins
Did you know how fun it is for a wooden unicorn figure to eat a muffin image on a die? I didn’t, either, until I discovered that this can easily make kids appreciate that they just rolled a zero.
Unicorn Glitterluck Manufacturer’s Information
Before I go and Monte-Carlo analyze the game for you, here are the most important things about the game and its manufacturer:
- Name: Unicorn Glitterluck: Cloud Crystals
- Number of players: 2 to 4
- Recommended player age: 3 to 99
- Duration of a typical game: 10 minutes
- Author: Kristin Mückel
- Illustrations: Stephanie Roehe
- Copyright: HABA Games
 , Bad Rodach, 2014
, Bad Rodach, 2014 - Weblink: https://www.habausa.com/unicorn-glitterluck-cloud-crystals/

- pdf game instructions: directly from HABA

My Recommendation
A perfect board game for little kids to learn and understand game mechanics that go beyond just rolling a die and moving along. At the same time, the objective seems to fascinate kids, because they need to understand where winning comes from instead of just racing to the finish line.
If your kid likes unicorns, nothing much can go wrong here, but also if they don’t, there are a number of very likeable things and moments about the game. I wholeheartedly recommend this to any board-game loving family with young kids.
Why I Decided to run a Monte-Carlo Simulation of this Game
Now, let’s have some fun, shall we? Those were my thoughts, when I decided to run a Monte-Carlo simulation of Unicorn Glitterluck. The general point of such a simulation is the following:
of Unicorn Glitterluck. The general point of such a simulation is the following:
Games of chance (like card games or games with dice) can be investigated by using probability theory
(like card games or games with dice) can be investigated by using probability theory . For each single roll of one of the dice, for example, we can compute the probability of each outcome very easily. However, when we concatenate lots of such rolls with the blue die and then also would like to calculate the outcomes for the various board positions and rolls of the pink die, using rainbow slides, etc., this becomes much too complicated much too quickly.
. For each single roll of one of the dice, for example, we can compute the probability of each outcome very easily. However, when we concatenate lots of such rolls with the blue die and then also would like to calculate the outcomes for the various board positions and rolls of the pink die, using rainbow slides, etc., this becomes much too complicated much too quickly.

Monte-Carlo simulation essentially plays lots and lots of games for us inside a computer and gives us the outcomes for each of them. What is most helpful to do with simulations like this, is to aggregate statistics about various numbers of interest. Here are a few examples:
- How many dice rolls are necessary to complete the game on average?
- How many crystals does the winner have on average?
- How many crystals are collected by all unicorns in the game in total, on average?
- How often, on average, does the finisher NOT win the game?
- How likely is a tie for first place?
Monte-Carlo-Simulation of Unicorn Glitterluck: Cloud Crystals
I programmed this Monte-Carlo simulation in python , using a standard installation together with the packages numpy
, using a standard installation together with the packages numpy and scipy
and scipy for the analysis as well as matplotlib
for the analysis as well as matplotlib for making the graphics.
for making the graphics.
Monte-Carlo-Simulation Setup
The setup of a Monte-Carlo simulation has a few important parameters. The first is the number of samples to use. This is basically the number of groups of games the computer should play. The second is the sample size, which is the number of games in each group (sample) that the computer will play.
For this particular case, I ran 50 samples of 1 Million games each, which are reasonable numbers (just trust me on this). They provide good enough precision without costing too much time to run.
Interesting Questions to Ask
I’ve already written down a number of fun and interesting questions above. Now, we’ll look at some answers, finally.
Number of Winner’s Crystals
The number of crystals that the winner of this game has collected on average is … 11.47. How do I know that? First of all, we can look at any particular sample to see the distribution of the winner’s number of crystals from the minimal number of 4 up to 20 and beyond (at least in theory, but the probabilities get very low very fast). Here it is:
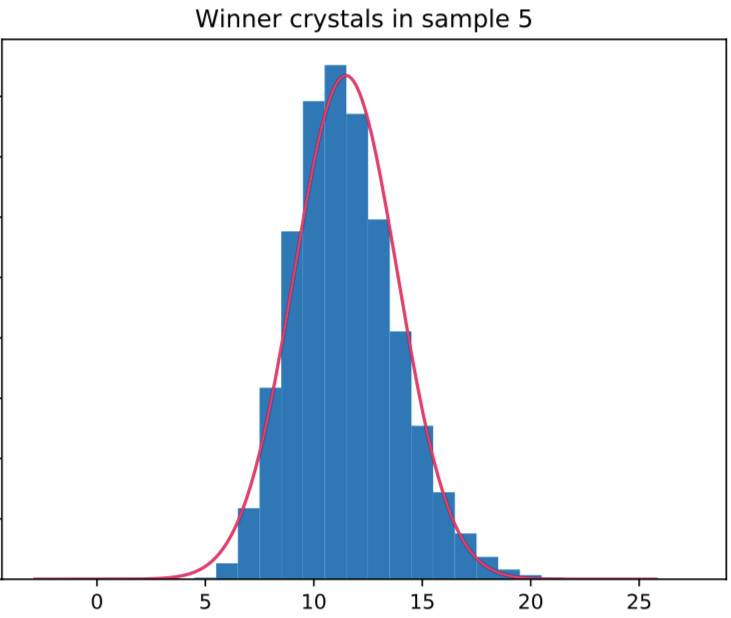
The blue bars indicate the relative amount of game outcomes for which the winner had the number of crystals noted on the bottom horizontal axis, which is called a probability distribution. The pink curve is a Gaussian fit of the data, which, apparently, is not quite Gaussian (normally distributed), but close enough to have the curve there.
From the highest bar and the peak of the curve we can see that the maximum is between 11 and 12, but we don’t know where exactly. And here is, where the different samples come into play. From the collection of samples, we can create another figure that gives us the distribution of the number we are looking at (the peak in the curve), plotted across the samples. Here is what that looks like:
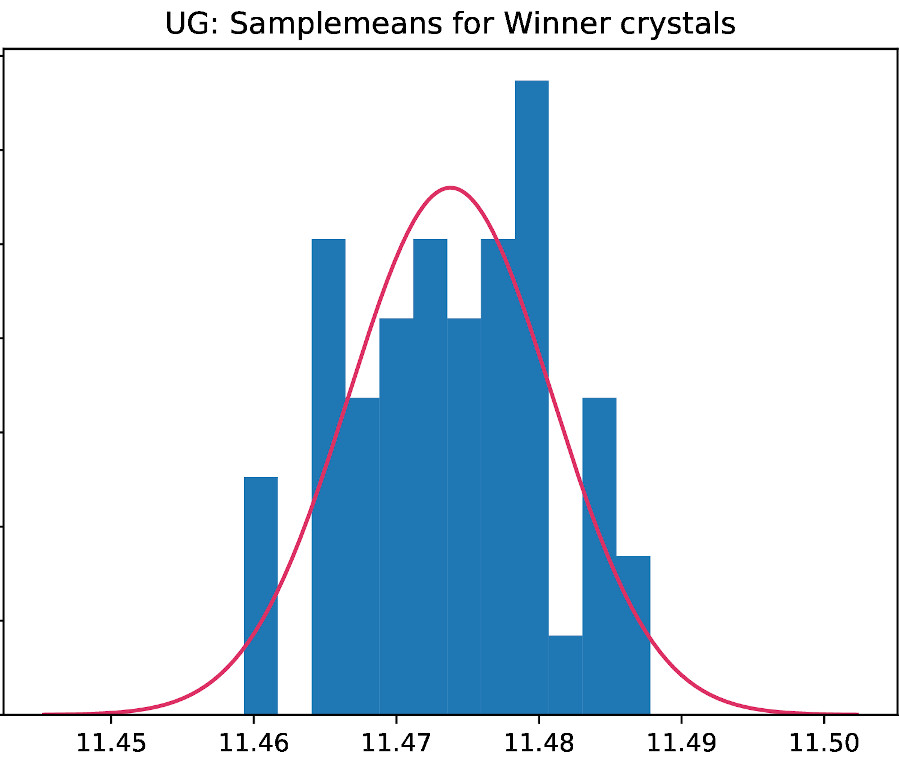
From this graphic, we can now see, where the average number comes from, which I quoted above. The same principles can be applied to other interesting numbers, a few of which are shown in the following.
Number of Total Crystals Collected by All Players
One number, which I found particularly interesting, is the total number of crystals collected by all unicorns in the game. Why did I find that interesting? Simply, because there is a passage in the game instructions that talks about what happens when the players run out of crystals during a game. Since there are 60 crystals in the reservoir, I was curious how often that was going to happen.
The answer is … probably not during our lifetime, because the average for the total number of crystals collected by four playing unicorns is … 30.77. And beyond this number, the probability drops. Look at this:
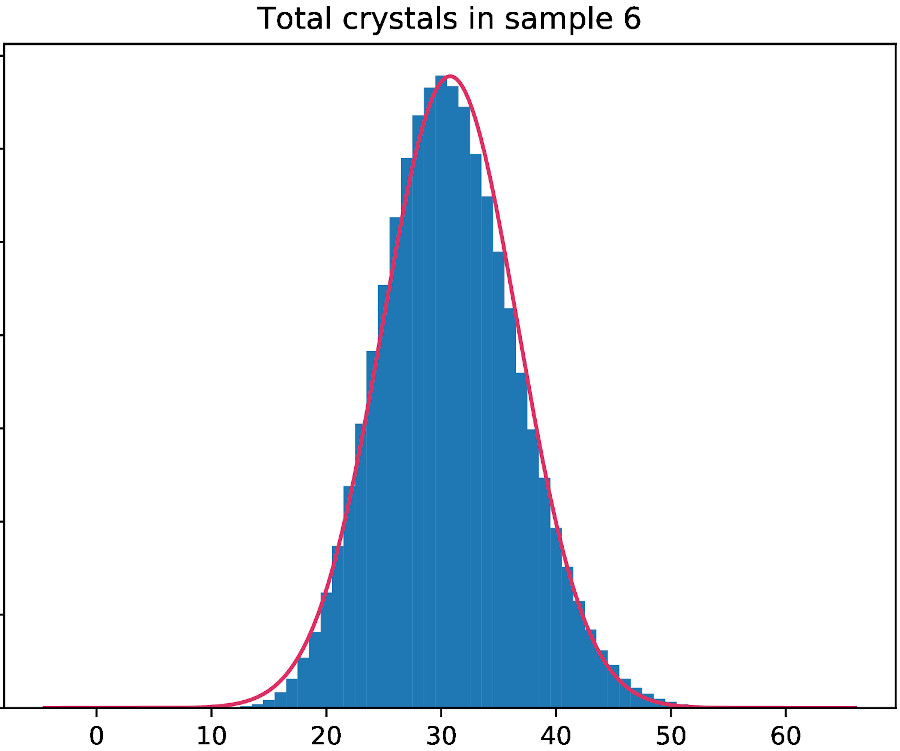
There is not much left of the probability beyond 55 total crystals, so I doubt that we would run out of crystals in a real game any time soon. If you want a concrete number for how often the total number of crystals exceeded 60 in my samples, here you go: a handful in a million.
By the way, the theoretical (and practical) minimum for the number of total crystals in a game is 5. Can you figure out why that is, looking at the game board above?
And for completeness: The average number quoted above comes from the sample means again, but I don’t want to bore you, so we move on to the next question:
How Often Does the First Finisher Not Win?
This is really interesting. While one of the unicorns may race ahead fast but skip all the pink clouds and thus end up with only 4 crystals at the end of the game board, the others could stop at every pink cloud and collect crystals like crazy, and thus easily win. Ok, now we see how it is possible, but how likely is that?
The answer to the question, how often the finisher also wins the game, is … 78.5%. So, in more than 20% of games, the winner is one of those unicorns, which don’t finish first.
